







ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №11-14.
Тема: Изолированные особые точки однозначного характера..
Ряды Лорана.
1. Пусть
функция ![]() регулярна в кольце 0<
регулярна в кольце 0<![]() <
<![]() (
(![]() <
<![]() <
<![]() , если
, если ![]() ), но не
определена в самой точке
), но не
определена в самой точке ![]() . В этом случае точку
. В этом случае точку ![]() называют изолированной особой точкой
однозначного характера для функции
называют изолированной особой точкой
однозначного характера для функции ![]() . По поведению функции
вблизи точки
. По поведению функции
вблизи точки ![]() различают три вида изолированных точек
особого характера:
различают три вида изолированных точек
особого характера:
1. Если 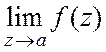 существует и конечен, то
существует и конечен, то ![]() устранимая особая точка;
устранимая особая точка;
2. Если 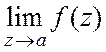 существует, но равен бесконечности, то
существует, но равен бесконечности, то ![]() называется полюсом функции
называется полюсом функции ![]() ;
;
3. Если 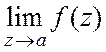 не существует, то точка
не существует, то точка ![]() называется существенно особой точкой
функции
называется существенно особой точкой
функции ![]() .
.
Определить тип
особой точки ![]() помогают теоремы
помогают теоремы
Теорема
1. Для того, чтобы изолированная особая точка ![]() была
устранимой особой точкой функции
была
устранимой особой точкой функции ![]() , необходимо и
достаточно, чтобы функция
, необходимо и
достаточно, чтобы функция ![]() была непрерывной и
ограниченной в некоторой проколотой окрестности точки
была непрерывной и
ограниченной в некоторой проколотой окрестности точки ![]() .
.
Теорема
2. Для того, чтобы точка ![]() (
(![]() ) была полюсом
) была полюсом ![]() ,
необходимо и достаточно, чтобы эта функция представлялась в виде
,
необходимо и достаточно, чтобы эта функция представлялась в виде ![]() ,
, ![]() , где
, где ![]() - функция, регулярная в точке
- функция, регулярная в точке ![]() (
(![]() ,
, ![]() , где
, где ![]() -
функция, регулярная в точке
-
функция, регулярная в точке ![]() ). Целое число
). Целое число ![]() называется порядком полюса
называется порядком полюса ![]() (
(![]() ).
).
2. Теорема
3. Функция ![]() , регулярная в кольце
, регулярная в кольце ![]() :
: ![]() представляется
в этом кольце сходящимся степенным рядом
представляется
в этом кольце сходящимся степенным рядом 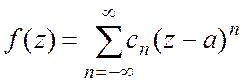 , где
, где 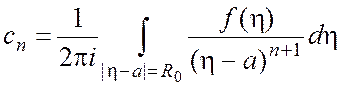 ,
, ![]() ,
, ![]() . Ряд
. Ряд 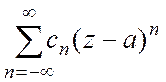 называется
рядом Лорана для функции
называется
рядом Лорана для функции ![]() в окрестности точки
в окрестности точки ![]() .
.
Ряд Лорана
называется сходящимся в точке ![]() , если в этой точке
сходятся ряды
, если в этой точке
сходятся ряды 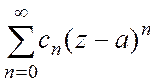 и
и 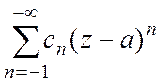 .
.
Главной
частью ряда Лорана в окрестности особой точки, конечной или
бесконечной, называется сумма всех тех и только тех членов ряда Лорана, которые
стремятся к бесконечности при ![]() .
.
Главная часть-
функция, регулярная во всей комплексной плоскости, кроме точки ![]() .
.
Правильной
частью ряда Лорана в окрестности особой точки ![]() называется
разность между
называется
разность между ![]() и главной частью ряда Лорана.
и главной частью ряда Лорана.
Правильная
часть ряда Лорана- функция, регулярная в точке ![]() .
.
3. Теорема
4. Для того, чтобы изолированная особая точка ![]() была
устранимой особой точкой функции
была
устранимой особой точкой функции ![]() , необходимо и
достаточно, чтобы главная часть ряда Лорана в окрестности точки
, необходимо и
достаточно, чтобы главная часть ряда Лорана в окрестности точки ![]() была тождественным нулем.
была тождественным нулем.
Теорема
5. Для того, чтобы изолированная особая точка ![]() была
полюсом функции
была
полюсом функции ![]() , необходимо и достаточно, чтобы
главная часть ряда Лорана в окрестности точки
, необходимо и достаточно, чтобы
главная часть ряда Лорана в окрестности точки ![]() содержала
лишь конечное число
содержала
лишь конечное число ![]() членов,
членов, ![]() -
порядок полюса.
-
порядок полюса.
Теорема
6. Для того, чтобы изолированная особая точка ![]() была
существенно особой точкой функции
была
существенно особой точкой функции ![]() , необходимо и достаточно,
чтобы главная часть ряда Лорана в окрестности точки
, необходимо и достаточно,
чтобы главная часть ряда Лорана в окрестности точки ![]() содержала
бесконечное число членов.
содержала
бесконечное число членов.
Определение
Точка ![]() называется точкой сгущения полюсов функции
называется точкой сгущения полюсов функции
![]() , если
, если ![]() регулярна
в некотором кольце 0<
регулярна
в некотором кольце 0<![]() <
<![]() , за исключением бесконечного числа
полюсов
, за исключением бесконечного числа
полюсов ![]() , таких, что
, таких, что 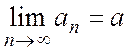 .
.
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №15,16.
Тема: Вычисление вычетов.
Пусть функция ![]() регулярна в проколотой окрестности точки a (a¹¥), т.е. в кольце 0<|z-a|<r. Вычетом
функции
регулярна в проколотой окрестности точки a (a¹¥), т.е. в кольце 0<|z-a|<r. Вычетом
функции ![]() в точке a (a¹¥)
называется величина
в точке a (a¹¥)
называется величина 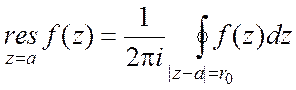 , где число 0<r0<r, и
окружность проходится в положительном направлении.
, где число 0<r0<r, и
окружность проходится в положительном направлении.
Пусть функция f(a) регулярна в кольце r<|z|<¥. Вычетом функции ![]() в бесконечности называется величина
в бесконечности называется величина 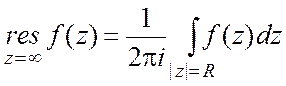 , где число
, где число ![]() >r и окружность проходится по ходу часовой стрелки.
>r и окружность проходится по ходу часовой стрелки.
Согласно теореме
Коши 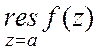 =0, если a-
точка регулярности функции
=0, если a-
точка регулярности функции ![]() . Вычет в бесконечности
может быть отличен от нуля даже в случае, когда функция регулярна в
бесконечности.
. Вычет в бесконечности
может быть отличен от нуля даже в случае, когда функция регулярна в
бесконечности.
Для вычисления
вычетов полезно утверждение: вычет функции ![]() в точке
в точке
![]() равен коэффициенту
равен коэффициенту ![]() ряда
Лорана для функции
ряда
Лорана для функции ![]() в окрестности точки
в окрестности точки ![]() .
.
Основные формулы для вычисления вычетов в полюсе:
1. Если ![]() имеет
имеет ![]() полюсом
первого порядка, тогда
полюсом
первого порядка, тогда 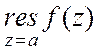 =
=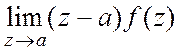 .
В частности, если
.
В частности, если 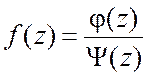 , где
, где ![]() и
и ![]() - регулярные в точке
- регулярные в точке ![]() функции,
функции, ![]() ,
, ![]() =0,
=0, ![]() , то
, то 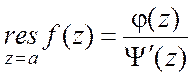 .
.
2. Если ![]() - полюс
- полюс ![]() -го
порядка функции
-го
порядка функции ![]() , то
, то 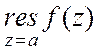 =
=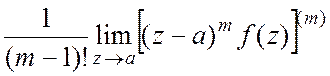 . В частности, если
. В частности, если 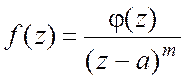 ,
,
![]() - регулярная в точке
- регулярная в точке ![]() функция, то
функция, то 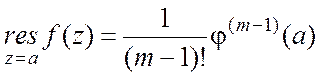 .
.
3. Пусть ![]() регулярна в точке
регулярна в точке ![]() .
Тогда
.
Тогда 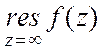 =
=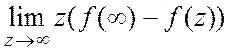 .
.
4. Пусть ![]() представима в виде
представима в виде ![]() ,
где
,
где ![]() регулярна в точке
регулярна в точке ![]() =0.
Тогда
=0.
Тогда 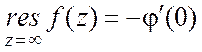 .
.
5. Пусть 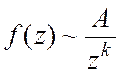 ,
, ![]() ,
, ![]()
![]()
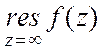 =
=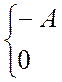
ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №17-19.
Тема: Вычисление интегралов по замкнутому контуру.
Задачи на этих практических занятиях решаются с помощью теоремы о вычетах:
Пусть функция ![]() регулярна в области
регулярна в области ![]() расширенной комплексной плоскости, за
исключением конечного числа точек
расширенной комплексной плоскости, за
исключением конечного числа точек ![]() ,
, ![]() , являющихся изолированными особыми точками
однозначного характера, и непрерывна вплоть до границы
, являющихся изолированными особыми точками
однозначного характера, и непрерывна вплоть до границы ![]() области
области
![]() , за исключением тех же точек. Граница
области предполагается состоящей из конечного числа кусочно-гладких замкнутых
кривых. Тогда
, за исключением тех же точек. Граница
области предполагается состоящей из конечного числа кусочно-гладких замкнутых
кривых. Тогда 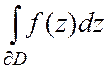 =
=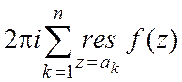 , если
граница обходится в положительном направлении.
, если
граница обходится в положительном направлении.
Если область ![]() содержит
содержит ![]() , то она
причисляется к точкам
, то она
причисляется к точкам ![]() , даже если функция
, даже если функция ![]() регулярна в ней.
регулярна в ней.
При вычислении интегралов от функций, регулярных во всей комплексной плоскости, за исключением конечного числа изолированных особых точек однозначного характера, следует иметь в виду, что полная сумма всех вычетов такой функции (включая вычет в бесконечности) равна нулю.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.