ПРАКТИЧЕСКОЕ ЗАНЯТИЕ №20-23.
Тема: Вычисление интегралов с помощью вычетов.
Основная идея при вычислении определенных интегралов с помощью вычетов состоит в сведении таких интегралов к интегралам по замкнутому контуру. Контур выбирается таким образом, чтобы внутри него находились особые точки (полюсы) соответствующей рациональной подинтегральной функции.
1. Интегралы
вида I=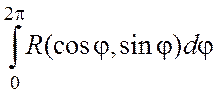 ,
где R(u,v)- рациональная функция от u и v.
,
где R(u,v)- рациональная функция от u и v.
Они сводятся к
интегралам по замкнутому контуру подстановкой ![]() . Тогда sinj=
. Тогда sinj=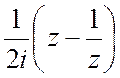 , cosj=
, cosj=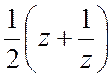 , dj=
, dj=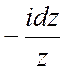 . Исходный интеграл
преобразуется к виду I=
. Исходный интеграл
преобразуется к виду I=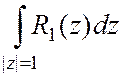 , где
, где 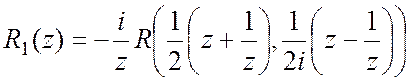 -рациональная
функция от z.
-рациональная
функция от z.
2. Интеграл
вида I=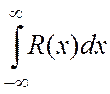 ,
R(x)-рациональная
функция. Для него выбирается вспомогательный замкнутый контур
,
R(x)-рациональная
функция. Для него выбирается вспомогательный замкнутый контур ![]() ,
,
где CR:
|z|=R, Imz³0.
Величина R выбирается
достаточно большой, такой, чтобы внутри контура находились все полюсы функции R(t), имеющие
положительную мнимую часть. Если R(z)~![]() ,
,
![]() , A¹0, k³2, целое, то интеграл I равен I=2pi
, A¹0, k³2, целое, то интеграл I равен I=2pi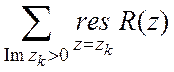 .
.
Замечание. Контур ![]() не обязательно имеет указанный вид, им
может быть, например, контур
не обязательно имеет указанный вид, им
может быть, например, контур ![]() : |z|=R, 0
: |z|=R, 0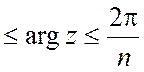 , n>2
-целое.
, n>2
-целое.
3. Интеграл вида I=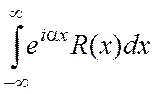 ,
, ![]() >0, R(x)- рациональная функция. Вспомогательный контур
>0, R(x)- рациональная функция. Вспомогательный контур ![]() имеет такой же вид, что и в пункте 2. Если
на действительной оси нет полюсов R(z) и R(z)~
имеет такой же вид, что и в пункте 2. Если
на действительной оси нет полюсов R(z) и R(z)~![]() ,
A¹0,
k³1,
то интеграл равен I=2pi
,
A¹0,
k³1,
то интеграл равен I=2pi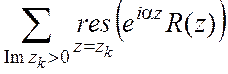 .
.
Замечания 1. Если a<0, то контур ![]() заменяется
симметричным относительно действительной оси и в правой части формулы
появляется знак "-".
заменяется
симметричным относительно действительной оси и в правой части формулы
появляется знак "-".
2. Контур G может иметь другой вид, например, контур ![]() может состоять из двух окружностей
радиусов r и R с общим центром в начале координат и двух отрезков [-r,-R] и [r,R].
может состоять из двух окружностей
радиусов r и R с общим центром в начале координат и двух отрезков [-r,-R] и [r,R].
4. Интеграл
вида 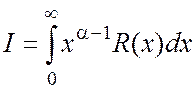 ,
, ![]() -нецелое
вещественное число, R(x)- рациональная функция. Для него вспомогательным
замкнутым контуром является контур, состоящий из двух окружностей радиусов r и R с центром в точке (0,0) и двух отрезков: l1:
-нецелое
вещественное число, R(x)- рациональная функция. Для него вспомогательным
замкнутым контуром является контур, состоящий из двух окружностей радиусов r и R с центром в точке (0,0) и двух отрезков: l1: ![]() -
верхний берег разреза и l2:
-
верхний берег разреза и l2: ![]() - нижний берег разреза. При этом r достаточно мало, R- достаточно велико, так, чтобы внутри контура
находились все полюсы функции R(z). При условии, что 0<a<k, где k определяется из асимптотического соотношения R(z)~
- нижний берег разреза. При этом r достаточно мало, R- достаточно велико, так, чтобы внутри контура
находились все полюсы функции R(z). При условии, что 0<a<k, где k определяется из асимптотического соотношения R(z)~![]() , A¹0, z-
целое, интеграл равен I=
, A¹0, z-
целое, интеграл равен I=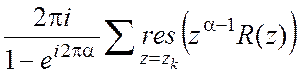 , zk-
все полюсы функции R(z).
, zk-
все полюсы функции R(z).
5. Интеграл
вида 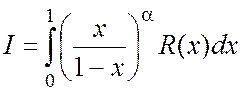 ,
, ![]() -нецелое
вещественное число, R(x)-
рациональная функция. Вспомогательный контур имеет вид "гантели":
интеграл рассматривается на всей комплексной плоскости за исключением разреза
по отрезку [0,1] и окружностей радиуса r вокруг точек 0 и 1 соответственно. Таким образом, контур
состоит из окружностей Cr: |z|=r,
-нецелое
вещественное число, R(x)-
рациональная функция. Вспомогательный контур имеет вид "гантели":
интеграл рассматривается на всей комплексной плоскости за исключением разреза
по отрезку [0,1] и окружностей радиуса r вокруг точек 0 и 1 соответственно. Таким образом, контур
состоит из окружностей Cr: |z|=r, ![]() :|z-1|=r и отрезков l1:
:|z-1|=r и отрезков l1:
![]() и l2:
и l2:
![]() , лежащих на верхнем и
нижнем берегах разреза соответственно.
, лежащих на верхнем и
нижнем берегах разреза соответственно.
Если -1<![]() <1 и
<1 и ![]() не
имеет полюсов на отрезке [0,1], то
не
имеет полюсов на отрезке [0,1], то 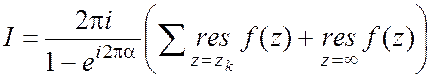 , zk-
все полюсы функции R(z)
и
, zk-
все полюсы функции R(z)
и ![]() =
=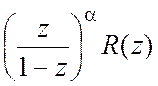 .
.
Подстановкой 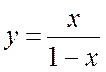 интеграл может быть сведен к интегралу
типа 4.
интеграл может быть сведен к интегралу
типа 4.
6. Интеграл
вида 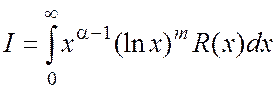 ,
, ![]() -действительное
число,
-действительное
число, ![]() 1, R(x)- рациональная функция, удовлетворяющая тем же
условиям, что и в случае 4. Вспомогательный контур интегрирования для интеграла
этого типа такой же, как и в случае 4: это две окружности радиусов r и R:
Cr: |z|=r, CК: |z|=R и два отрезка l1:
1, R(x)- рациональная функция, удовлетворяющая тем же
условиям, что и в случае 4. Вспомогательный контур интегрирования для интеграла
этого типа такой же, как и в случае 4: это две окружности радиусов r и R:
Cr: |z|=r, CК: |z|=R и два отрезка l1: ![]() и
l2:
и
l2: ![]() , лежащих на верхнем и нижнем
берегах разреза по положительной действительной оси соответственно.
, лежащих на верхнем и нижнем
берегах разреза по положительной действительной оси соответственно.
Обозначим через
![]() подинтегральную функцию на отрезке l1, через
подинтегральную функцию на отрезке l1, через ![]() -
подинтегральную функцию на отрезке l2:.
Тогда
-
подинтегральную функцию на отрезке l2:.
Тогда 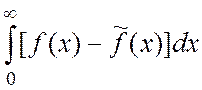 =
=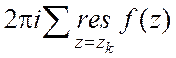 , где сумма берется по
всем полюсам функции
, где сумма берется по
всем полюсам функции ![]()
Возможны два случая
1. Число ![]() -нецелое. Тогда левая часть последнего
равенства содержит
-нецелое. Тогда левая часть последнего
равенства содержит ![]() ; интегралы (при
; интегралы (при ![]() >1) вида
>1) вида 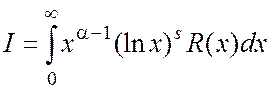 ,
, ![]() . Последние связаны рекуррентными соотношениями,
позволяющими вычислить интеграл
. Последние связаны рекуррентными соотношениями,
позволяющими вычислить интеграл ![]() .
.
2. Число ![]() - целое. Тогда для вычисления интеграла в
качестве подинтегральной функции следует взять
- целое. Тогда для вычисления интеграла в
качестве подинтегральной функции следует взять ![]() .
.
Рассмотрим примеры.
1. Вычислить
интеграл I=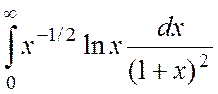 .
.
a=1/2, 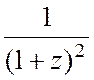 ~
~![]() , z®¥ Þ k=2.
Поскольку aÎ(0,2), то
, z®¥ Þ k=2.
Поскольку aÎ(0,2), то 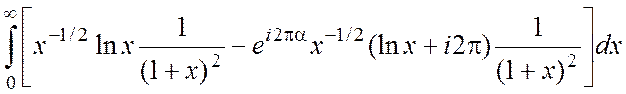 =
=
=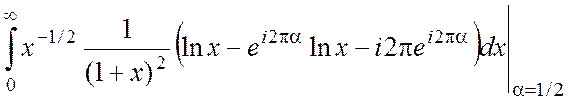 =
=
=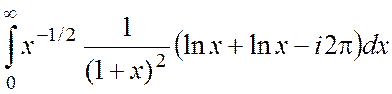 Þ 2I+2pi
Þ 2I+2pi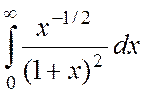 =2pi
=2pi![]() f(z) и f(z)=
f(z) и f(z)= .
.
Точка z=
-1 является для f(z) полюсом
второго порядка, поэтому ![]() f(z)=
f(z)=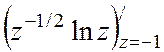 =
= 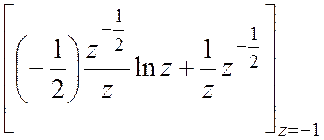 , где
, где
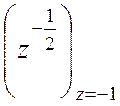 =
=![]() = -i,
= -i, ![]() =ip.
Следовательно,
=ip.
Следовательно, ![]() f(z)=
f(z)=![]() +i.
Имеем: 2I+2pi
+i.
Имеем: 2I+2pi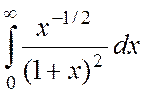 =
-2p+ip2. Приравнивая мнимые и
действительные части выражения, находим I= -p,
=
-2p+ip2. Приравнивая мнимые и
действительные части выражения, находим I= -p, 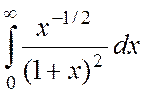 =
=![]() .
.
2. Вычислить интеграл I=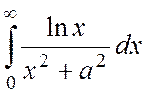 , a>0.
, a>0.
Для получения результата следует
вычислить интеграл I1=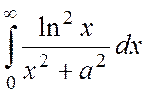 указанным
выше способом:
указанным
выше способом: 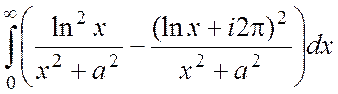 = -i4p
= -i4p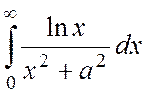 + +4p2
+ +4p2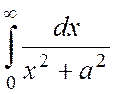 Þ -4pi I+ 4p2
Þ -4pi I+ 4p2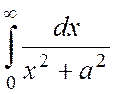 =2pi
=2pi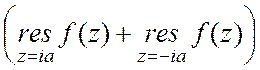 , причем f(z)=
, причем f(z)=![]() . Точки ±ia являются полюсами первого порядка для f(z), поэтому
. Точки ±ia являются полюсами первого порядка для f(z), поэтому 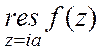 =
=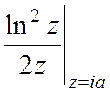 =
=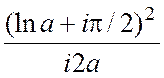 ;
; 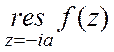 =
= 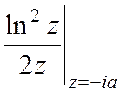 =
=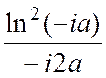 = =
= =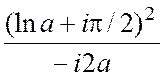 ;
;
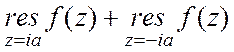 =
=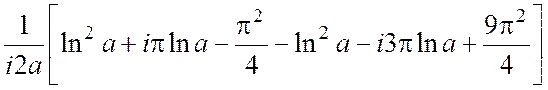 = =
= =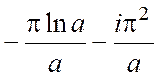 ;
; 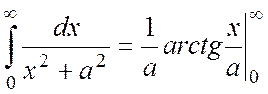 =
=![]() . Таким образом, имеем равенство:
. Таким образом, имеем равенство:
I+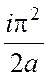 =
=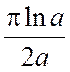 +
+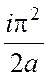 Þ I=
Þ I=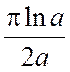 .
.
Для данного
примера в силу четности функции R(z)=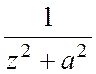 контуром интегрирования можно взять контур Gr,R, описанный в замечании 2 для интегралов третьего
типа. Поскольку интеграл этого типа сходится при тех же условиях на функцию R(z), что и интеграл
четвертого типа, то имеем:
контуром интегрирования можно взять контур Gr,R, описанный в замечании 2 для интегралов третьего
типа. Поскольку интеграл этого типа сходится при тех же условиях на функцию R(z), что и интеграл
четвертого типа, то имеем:
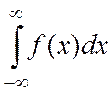 =2pi
=2pi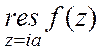 , где f(z)=
, где f(z)=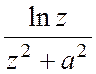 и lnz- регулярная ветвь логарифма, принимающая действительные
значения при z=x>0.
и lnz- регулярная ветвь логарифма, принимающая действительные
значения при z=x>0.
Здесь 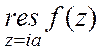 =
=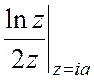 =
=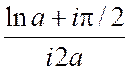 ,
, 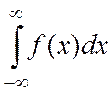 =
= 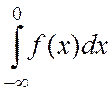 +
+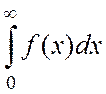 =
=
=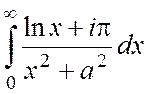 +
+ 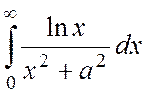 =2I +ip
=2I +ip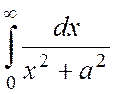 ; итак, 2I+ip
; итак, 2I+ip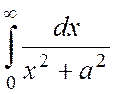 =
=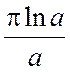 +
+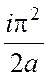 ÛI+
ÛI+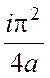 =
= 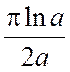 +
+ 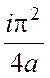 Þ I=
Þ I=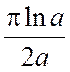 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.