








Лекция № 1.
Теория вероятностей и математическая статистика.
Предмет теории вероятности, математическая статистика. Комбинаторика.
1. Предмет теории вероятности, математическая статистика.
S – множество некоторых условий. В результате S появляется событие А:
а) При каждом точном воссоздании условий S возникает А.
![]()
Это детерминированный подход, а событие А – не случайно.
б) При воссоздании условий S событие А может произойти, а может не произойти.
![]()
![]() .
.
Это случайный подход, А – случайное событие.
а) Утверждается, что при каждом осуществлении условий S обязательно наступает А. Это бывает, например, в классической механике, А именно: если заданы начальные координаты тела, начальные скорость и сила, действующие на тело, то движение тела будет происходить однозначно и вполне определенно, т.е. в каждый последующий момент времени t>t0 можно указать координаты этого тела и его скорость. Эти события называются детерминированными (неслучайными), они происходят каждый раз, как только воссоздаются условия S.
б) В этом подходе к исследованию задачи утверждается, что при каждом воссоздании условий S события А может наступить, а может и не наступить. Например, если подбрасывать монету в одних и тех же условиях, стрельба в тире. В таких случаях для описания А вводят меру случайности этого события.
Р=Р(А/S)
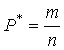 -
относительная частота А в данной серии испытаний.
-
относительная частота А в данной серии испытаний.Пусть n1=100. Фиксируем p1*, n2=100, p2* … === последовательность pi*.
Вероятностью А называется
![]()
Событие, наступающее при осуществлении условий S, с начальной вероятностью называется случайным событием.
Закономерности, описывающие связи между условиями S и наступлением А в б) называется статистическими закономерностями.
Предмет теории вероятности – изучение свойств вероятности событий и статических закономерностей.
Математическая статистика – раздел математики, посвященный математическим методам систематизации, обработки и использования статистических данных для научных и практических целей. Например, статистическими данными могут быть результаты переписи населения. В данном случае можно интересоваться: числом жителей города возрастом до 10 лет, призывного возраста, …
Математическая статистика рассматривает некоторые признаки объектов, множество значений которых образуют генеральную совокупность (совокупность всех значений выделенного признака).
Выборка из генеральной совокупности – множество наблюдаемых случайных значений изучаемого признака. Чтобы по результатам выборки можно было делать достоверные выводы, нужно чтобы она была репрезентативной, т.е. должна содержать в себе (отражать) все основные статистические закономерности генеральной закономерности. Для этого необходимы элементы выборки получать случайным, независимым друг от друга, способом.
Предметом математической статистики является формальная математическая сторона статистических методов, безразличная к специфичной природе изучаемых объектов, позволяющая делать объективные (достоверные) выводы о свойствах генеральной совокупности.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.