Два игрока ведут игру. Первый бросает кость, записывает число и не показывает второму. Второй игрок должен угадать число, которое записал первый.
А – угадал, что первый записал ![]() Первый
сообщил некоторую информацию о выпавшем числе второму.
Первый
сообщил некоторую информацию о выпавшем числе второму.
В – записал четное число.
А/В – событие А при условии, что произошло В. Р(А/В) – условная вероятность.
Р(А/В)=![]()
При
наличии дополнительной информации о событии А, его вероятность меняется Е, |Е| - число элементов пространства элементарных событий
Р=![]() .
.
А - |А| - которому благоприятствуют |А| элементарных исходов.
В - |В|
![]()
 А×В - |А×В|
А×В - |А×В|
![]()
![]()

![]()
![]() Р(А/В)=
Р(А/В)=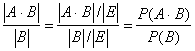 ,
,
|
Р(А/В)=![]() (1)
(1)
Пусть у нас имеется (Е, U, Р), А,ВÌU, причем Р(В)¹0. Тогда формула (1) называется формулой условной вероятности события А при условии, что событие В наступило.
Р(А/В) – означает функцию вероятности, определенное в нашем вероятностном пространстве.
События А и В называется независимым, если
Р(А/В)=Р(А) или Р(В/А)=Р(В) (2)
Теорема (о вероятности произведения). Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого при условии, что первое наступило
![]() -
зависимы. (3)
-
зависимы. (3)
Р(А×В)=Р(А) ×Р(В) (4)
(3) – может быть распространено на любое конечное множество событий.
![]() (3) /
(3) /
Определение. События Аi1, Аi2, …, Аis
из множества ![]() называются независимыми в
совокупности, если для " подмножества
называются независимыми в
совокупности, если для " подмножества
Аi1, Аi2, …, Аis Р(Аi1, Аi2, …, Аis)=Р(Аi1)×Р(Аi2)…Р(Аis)
![]() (4)
/
(4)
/
2. Совместность событий. Вероятность суммы событий.
Определение. События А и В называются совместными, если существует, по крайней мере, один элементарный исход данного опыта, который приводит и к наступлению события А и к наступлению события В.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.