Предмет теории вероятности, математическая статистика. Комбинаторика. Алгебра событий. Аксиоматическое определение вероятности. Вероятность пространства, страница 2

2.  Комбинаторика.

Х – некоторое множество различных объектов, n – количество объектов. Из этого множества мы можем выбрать k объектов.

            Выборка объема k (k-выборный) называется произвольная совокупность k объектов, взятая из множества Х.

Типы выборок:

1.  Перестановки.

Определение 1. Перестановкой называется любая n-выборка.

(1)  P_n=n! – число всех перестановок. n!=; 0!=1.

Пример.

abc                                                                          

            bac      

cab

      ….

           

           

2.  Размещение.

Определение 2. Размещением из n различных элементов по k элементам называется любая упорядоченная k-выборка.

            Размещением являются различными, если они различаются порядком следования элементов либо, по крайней мере, одним элементом.

(2)  - число всех размещений из n по k.

 Пример.                                                                                                                                 

                                                                                                                                     

            Сколько различных двузначных чисел с неповторяющимися цифрами можно составить из множества

.

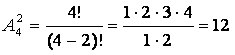            Если допустить повторение элементов в размещениях, то приходим к понятию размещений с повторениями.

(2)   - количество всех размещений с повторениями из n по k.

Пример.                                      ab ac bc aa cc

                                                  ba ca cb bb

                     было 12 +

                     11, 12, 33, 44.

Пример. Пусть Х – множество всех цифр от 0 до 9. Сколько существует различных 6-тизначных телефонных номеров.

            Это будут размещения с повторениями из 10 по 6:

3.  Сочетания.

Определение 3. Сочетанием из n различных элементов по k называется любая k-выборка из этих n элементов.

            Различными считаются те сочетания, которые различаются, по крайней мере, одним элементом.

(3)   - количество всех сочетаний из n по k.

Пример. . Найти