Кинематический расчет приводов главного движения со ступенчатым регулированием скорости, страница 7

Приемлемое решение будет при S_z = 84:

Особенности расчета чисел зубьев колес при различных мо­дулях передач одной группы

Иногда окружные усилия, передаваемые различными парами колес группы разнятся настолько значительно, что целесообразно брать для них различные модули, но и в таких случаях больше ; двух модулей в одной группе допускать не следует.

Если модули передач одной группы различны, то число зубьев ведущего колеса выражается через межосевое расстояние a_w сле­дующим образом:

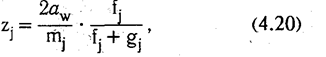
где m_j — модуль зубчатой передачи;

f_j и g_j — целые числа.

Число зубьев z. будет целым лишь при условии, когда

2а_w = Е*m_j* (f_j + g_j) , где Е — целое число. Следовательно, наи­меньшее удвоенное межосевое расстояние 2а_w, равно наименьше­му общему кратному произведений m_j (f_j + g_j). Очень часто это расстояние получается нереально большим, а сумма чисел зубьев сопряженных колес намного больше допустимой величины. По этой причине приходится находить наименьшее кратное модулей, увеличив его в некоторое целое число раз (до приемлемой конст­руктивной величины), и это число принимают за удвоенное меж­осевое расстояние. Тогда суммы чисел зубьев Sz =a_w/m_j будут целые числа, а рассчитанные числа зубьев z_j=2a_w/m_j*f_j/f_j+g_j и

z'_j =2a_w/m_j*g_j/f_j+g_j  будут получаться дробными и их надо будет округлять до целых чисел, сохраняя передаточные отношения.

Если полученная сумма зубьев сопряженных колес все же не обеспечивает точно заданные передаточные отношения, то нужно применять коррекцию зубьев, которая сводится к увеличению или уменьшению числа зубьев при сохранении диаметра начальной окружности зубчатого колеса. Величину коррекции можно допу­скать до 10—15%.

Рассмотрим пример расчета чисел зубьев колес при различных модулях передач в группе (рис. 4.11).

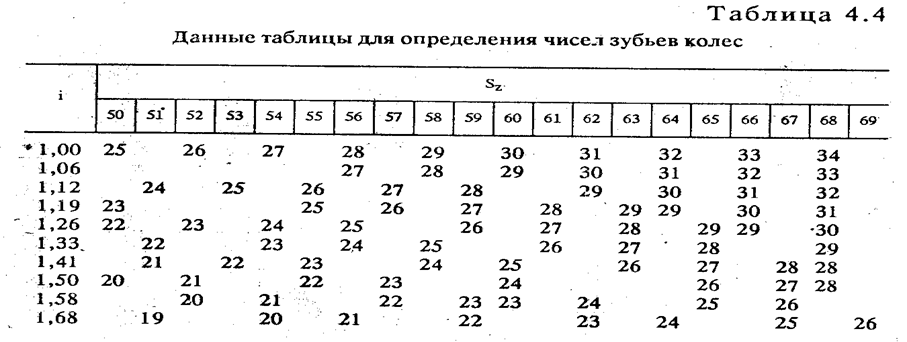
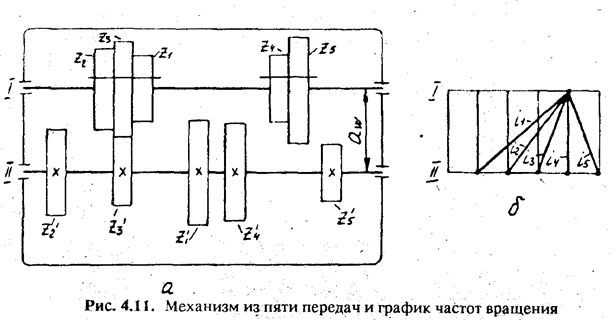
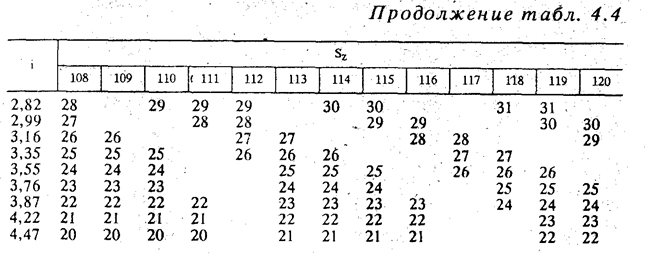
На рис. 4.11 показан механизм напять различных передач (случай на практике редкий, но, в принципе, возможный) и гра­фик частот вращения. При знаменателе геометрической прогрес­сии j = 1,41 передаточные отношения будут:

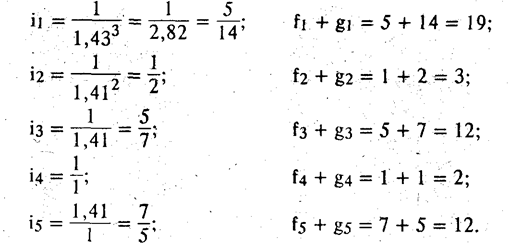
Предположим, трехступенчатый блок и сопряженные с ним зубчатые колеса имеют модуль m₁ = 3,5 мм, а двухступенчатый блок - модуль 

m₂ = 2.75 мм. Межосевое расстояние

Если удвоенное межосевое расстояние определять как наименьшее общее кратное произведений m_j (f_j + g_j), то получится очень боль­шая, практически неприемлемая величина. Поэтому находим крат­ное только одних модулей и, увеличив, принимаем его за удвоенное межосевое расстояние 2a_w = m₁* m₂ = 3,5 • 2,75 = 9,625. Увели­чим кратное модулей в целое число раз до реальных размеров, на­пример, в 32 раза. Тогда 2a_w = 9,625 • 32 = 308мм.

Находим расчетные суммы зубьев сопряженных колес S_z1 и S_z2;

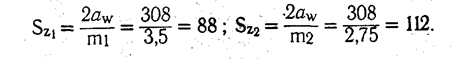
Рассчитываем числа зубьев сопряженных зубчатых колес по формулам

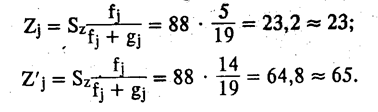
Тогда i₁=23/65=1/2,83 такое значение удовлетворяет заданному отношению

но для сохранения более точного передаточного отношения следу­ет принять z'₂ = 58, тогда величина коррекции составит

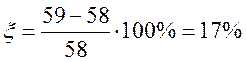 а передаточное отношение i₂=29/58=1/2.

Z₃=88*5/12=36.6»37; z¢₃=88*2/3=58.6»59, тогда i₃=37/51=1/1.38.

Чтобы получить более точное передаточное отношение примем

z'₃ = z₃ * 1,41 = 37* 1,41 = 52; величина коррекции составит

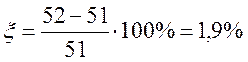 что вполне допустимо, а передаточное

отношение будет i₃ =37/52=1/1.405.  Расстояние между осями валов:

Для двухостальных передачс S_z2 ==112

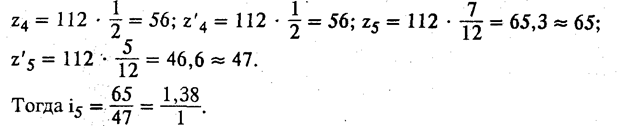
Для получения более точного передаточного отношения i₅ при­нимаем

z'₅ = 46, величина коррекции

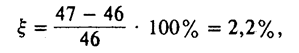
а передаточное отношение

Расстояние между осями валов

В результате расчета находим, что зубчатые передачи z₂/z¢₂, z₃/z¢₃ и z₅/z¢₅ должны иметь коррегированный зуб, причем коррекции может

подвергаться только одно зубчатое колесо из каждой пары. Изго­товление таких зубчатых колес никаких трудностей не представ­ляет, потому что нарезание их производится нормальным инстру­ментом.

,