Кинематический расчет приводов главного движения со ступенчатым регулированием скорости, страница 6

для первой переборной группы передач i₄ = 1/j³; i₅=1/1;

для второй переборной группы передач  i₆=1/ j⁴; i₇=j².

После того, как передаточные отношения всех передач, входя­щих в состав кинематической схемы, установлены, необходимо определить числа зубьев зубчатых колес.

ЛЕКЦИЯ 5  

4.4. Расчет чисел зубьев зубчатых передач

Расчет чисел зубьев групповых передач можно осуществлять методом наименьшего общего кратного или табличным способом. Метод наименьшего кратного наиболее приемлем для случая, ког­да передаточные отношения представляют собой отношения про­стых чисел.

Для сокращения номенклатуры зуборезного инструмента, сни­жения стоимости станка модули всех зубчатых передач одной и той же группы следует делать одинаковыми. В этом случае у тяже­ло нагруженных шестерен увеличивают ширину или изготавлива­ют их из более качественных материалов, сохраняя работоспособ­ность.

При расчете чисел зубьев наиболее типичным случаем являет­ся расчет группы передач, состоящей из прямозубых колес (угол наклона bj == 0) одного и того же модуля.

Метод наименьшего общего кратного

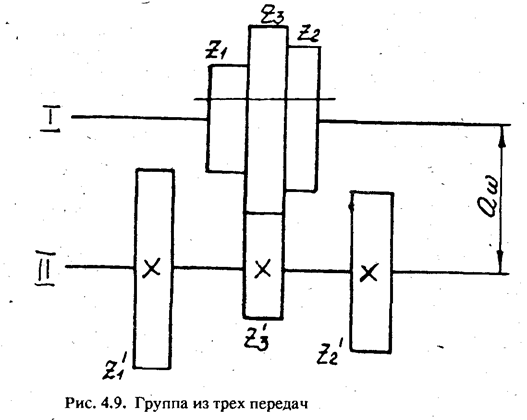
Так как межцентровое расстояние w для всех зубчатых колес группы является величиной постоянной (рис. 4.9) и равно

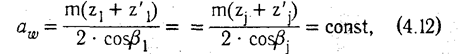
то при одинаковом модуле зубчатых колес должно быть справед­ливо соотношение

где    a_w — межцентровоерасстояние группы передач;

         m —модуль в мм;

        b_j — угол наклона зубьев;

:      Sz— сумма чисел зубьев сопряженных колес;

z_j и z’_j.—числа зубьев ведущего и ведомого колес.

Передаточное отношение пары зубчатых колес

Из уравнений (4.13) и (4.14) следует

Пусть ij = -^' = -^L, где f_j и g_j — простые числа. Тогда формулы для расчета чисел зубьев примут вид

Так как z_j и z'_j должны выражаться целыми числами, то сум­ма чисел зубьев S_z должна быть кратна (f_j + g_j), то есть

где К — наименьшее общее кратное всех сумм (f_j + g_j) рассчитыва­емой группы передач;

Е — целое число; Е = 1; 2; 3; ...

Если число зубьев шестерни, рассчитанное по формулам (4.16), получилось меньше допустимой величины, определяемой условием подрезания зубьев, то есть Z_min < 17¸18, то

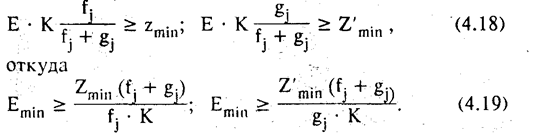
Значение E_min округляется до ближайшего большего целого числа. Если из конструктивных соображений окажется, что сумма зубьев недопустимо мала, то ее увеличивают в целое число раз до прием­лемой величины. С другой стороны, сумма зубьев S_z должна быть не больше 100—120.

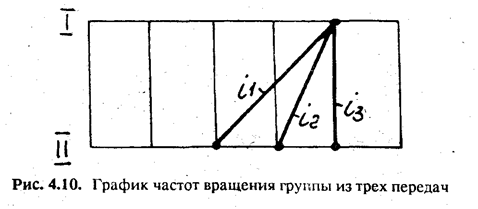
Пример. Рассчитать числа зубьев в основной группе передач по рис. 4.9 и 4.10. Знаменатель j = 1,26. Из графика (см. рис. 4.10) определяем передаточные отношения группы, состоящей из трех передач, и записываем их в табл. 4.3.

Для передаточного отношения i_min = 7/11, определим E_min, приняв z_min=18;

 E_min=18(7+11)/7*18»3; тогда сумма зубьев будет

S_z = Е' *К = 3 * 18 = 54. Пользуясь формулами (4.16), находим

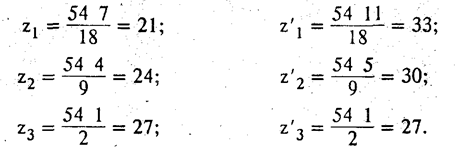
Расчет чисел зубьев в любой группе привода осуществляется

подобным образом.             .

Табличный метод

Для облегчения расчетов чисел зубьев групповых передач при­ведена табл. 4.4 с указанием чисел зубьев меньшего зубчатого ко­леса. Пустые клетки означают, что при данной сумме S_z переда­точное отношение не может быть выдержано в требуемых преде­лах с максимально допустимой погрешностью ±10 (j—1)%.

При определении чисел зубьев по табл. 4.4 для рассчитываемой группы передач выбирается сумма зубьев сопряженных колес S_z так, чтобы отношение чисел зубьев этой суммы  Z_j/Z¢_j обеспечиваловсе передаточные отношения сопряженных пар в данной группе. Сумма зубьев сопряженных колес S_z не должна быть больше 120.

Пример. Определить числа зубьев трех пар сопряженных зубча­тых колес, которые должны обеспечить передаточные отношения

Если по табл. 4.4 взять, например, Sz=76, то при

I₁=1/2.82; z₁:z¢₁=(76-20):20 а при i₂=1/2; и i₃=1/1.41  имеем пустые клетки. Следовательно, надо найти такое значение S_z, которое удовлетворяет всем трем передаточным отношениям.