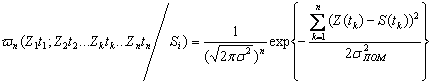Система связи. Назначение и виды кодирования, страница 8

        (3)

Подставляя выражения (2) и (3) в (1) получим:

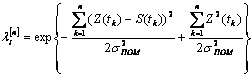
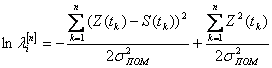
где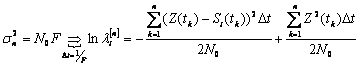

- спектральная плотность мощности.

Снимем принятое ограничение, т.е.  

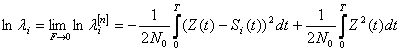   (4)

(4) – логарифм правдоподобия для n-мерного пространства.

Раскрывая, получим:

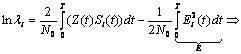
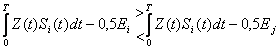      (5)

(S) – позволяет построить функциональную схему оптимального приёмника:

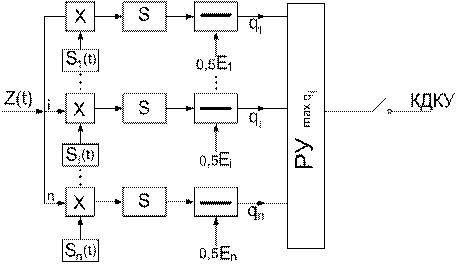
меняться на и на выходе выявляется эффект обратной работы

Подставляя (6) в (1) и проводя те же преобразования, приходим к тому же

Что показывает: при передаче разных сигналов и приходим к тем же вероятностям ошибки.

Т.О. вероятность правильности или неправильности правильного приёма не зависит от подаваемого сигнала.

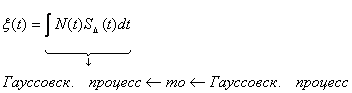
Нарисуем спектральную плотность этого процесса:

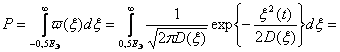
Введём новую переменную

После дифференцирования:

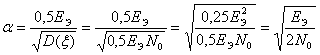
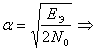
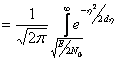
Формула Крампа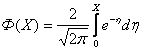

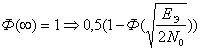
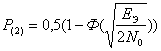 - для бинарных процессов

Вероятность зависит от соотношения сигнал/шум, от эквивалентной энергии

Особенности приёма ФМ-сигналов.

ФМ сигналы обладают максимальной помехоустойчивостью.

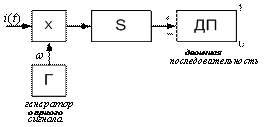
Проблема в том, чтобы сформировать опорный сигнал.

Схема Пистолькольса:

Стали применять эту схему, но её недостаток заключается в том, что под действием шума, фаза выходного сигнала может

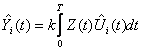
 если

Если , тогда нет необходимости использовать  и .