Предложим обозначать алфавит, как:

n – вероятность появления буквы (если бы они были равновероятны).

Энтропия – это среднее количество информации, передаваемое 1ой буквой алфавита.
![]() , H
– энтропия
, H
– энтропия
![]()
Свойства энтропии.
1. Энтропия величина положительная, действительная и ограниченная.
Доказательство: ![]()
![]()
![]() - MAX
- MAX
![]()
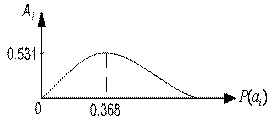
2. Энтропия бинарного сообщения максимальна, когда p=0,5
![]()
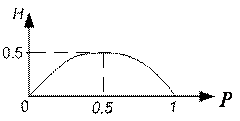
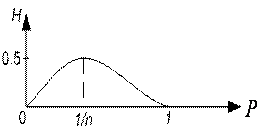
3. Энтропия дискретного ![]() алфавита
максимальна для равновероятного сообщения.
алфавита
максимальна для равновероятного сообщения.
Из свойства следует, что мера Хартли даёт завышенное количество информации.
4. Энтропия нескольких независимых источников ![]() равна сумме их энтропий.
равна сумме их энтропий.
![]()
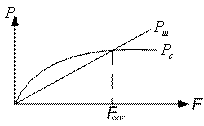
![]() - пропускная способность
- пропускная способность
![]() - характеризует утечку
информации в КС.
- характеризует утечку
информации в КС.
![]() - имеет место наличие
притока ложной информации
- имеет место наличие
притока ложной информации
Эти два процесса идут одновременно, и они взаимосвязаны, нельзя изменять один процесс, не затрагивая другой.
![]()
![]()
Информационные характеристики для непрерывных сообщений.
При оценке информационных процессов при передаче информационных сообщений существует 2а подхода:
-учитывая связь непрерывных и дискретных сообщений по Т. Котельникова, можно преобразовать из непрерывного в дискретный и наоборот.
-вводится специальная информационная характеристика для оценки непрерывного сообщения - дифференциальная энтропия: произв. оценка всех информационных характеристик и каналов.
Сама характеристика дифференциальной энтропии получается путём предельного перехода из дискретной энтропии в дифференциальную.
Оценка количества информации передаваемой непрерывным сообщением по 1му способу:
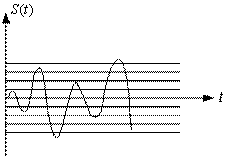
F – ширина спектра и пусть в канале действует аддитивная помеха.
Будем использовать меру Хартли ![]()
Осуществим
квантование по Т. Котельникова с шагом ![]() u
u
![]()
![]() - иначе, нет смысла в
квантовании.
- иначе, нет смысла в
квантовании.![]()
![]()
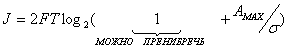
![]()
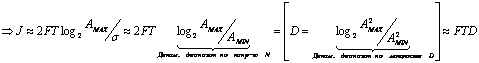 т. е.
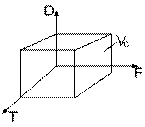
т. е. ![]() - объём сигнала
- объём сигнала
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.