Сигналы, обладающие этими свойствами образуют пространство.
Пространство может быть линейное и нелинейное, одномерно,
двумерное…, n-мерное,![]() -мерное.
К n-мерному и
-мерное.
К n-мерному и ![]() -мерному
мы приходим индуктивным путём, рассматривая свойства одномерного пространства
более высокого порядка т.е. гиперпространства.
-мерному
мы приходим индуктивным путём, рассматривая свойства одномерного пространства
более высокого порядка т.е. гиперпространства.
Гиперпространство – пространство высоких размерностей.
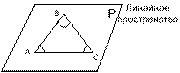
Пространство элементов ![]() является
линейным, если определено правило сложения элементов пространства и правило
умножения элементов пространства на скаляр удовлетворяющие этим правилам:
коммутативность
является
линейным, если определено правило сложения элементов пространства и правило
умножения элементов пространства на скаляр удовлетворяющие этим правилам:
коммутативность
ассоциативность
дистрибутивность
Пространство считается линейным, если ![]() причём
причём ![]() .
.
В таком пространстве всегда существует нулевой элемент ![]() , а так же существует противоположный
элемент
, а так же существует противоположный
элемент ![]()
Условия линейности:
1.![]()
2.если часть области скаляр ![]() ,
то
,
то ![]() ,
,
а ![]()
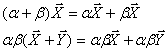
Если пространство удовлетворяет этим 2м условиям, то оно линейное.
![]()
![]()
Нелинейное пространство

![]()
Нелинейное пространство – пространство Римана, расписывается на поверхности в виде граммофонной трубы.
Пространство Лобачевского имеет вид сферы.
![]()
![]()
Если использовать ансамбль сигналов с равной энергией, когда
нам не нужны вычитающие устройства (![]() ).
).
Если в схеме используется 2а сигнала, то
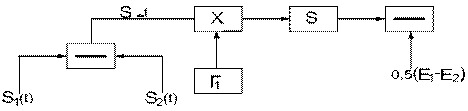
Представленная схема представляет собой корреляционный вариант схемы. Т.к. согласованный фильтр в момент времени даёт тот же самый результат, что и коррелятор, то можно организовать многоканальную схему фильтрового типа:
При использовании сигналов равной энергии отпадает необходимость использовать вычитатель.
![]() - для согласованного
фильтра.
- для согласованного
фильтра.
Существует 2а свойства согласованных фильтров:
Согласованный фильтр будет
согласован, если его импульсная характеристика ![]() является
зеркальным отображением сигнала, относительно
является
зеркальным отображением сигнала, относительно ![]() :
: ![]() .
.
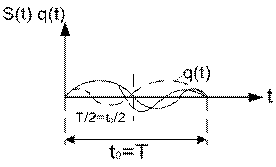
Условие ![]() является
физической реализуемости согласованного фильтра для обработки сигналов в
реальном времени.
является
физической реализуемости согласованного фильтра для обработки сигналов в
реальном времени.
![]()
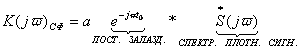
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.