когерентном приёме.
Потенциальная помехоустойчивость – критерий, характеризующий качество приёма сигнала.
Критерием является вероятность ошибки.
Рассмотрим потенциальную помехоустойчивость для бинарных
сигналов: ![]()
![]()
Получим математическую формулу для нахождения ошибки.
Потенциальная помехоустойчивость будет вводиться при оптимальной процедуре:
![]() (1)
(1)
Если данное условие не выполняется, то будем определять вероятность ошибки
![]() (2)
(2)
Подставляя (1) в (2) получим:
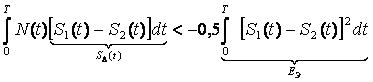 (3)
(3)
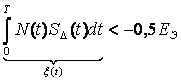 (4)
(4)
![]() (5)
(5)
Если неравенство (3),(4),(5) то они определяют вероятность ошибки при принятии решений.
произвольно определяется шумом
воспроизведения ![]() и
и ![]() -
когда
-
когда ![]() Гауссово:
Гауссово:
![]()
![]()
![]()
Найдём для Гауссовского источника
![]()
![]() тогда
тогда ![]()
Т.О. эквивалентность сообщений при заданной квадратической ошибки определяется соотношением сигнал/шум.
Пропускная способность сообщения будет определяться как:
![]()
![]() - техническая скорость.
- техническая скорость.
![]()
![]()
Количество информации: ![]()
Избыточность: 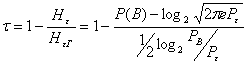
Т.О. ![]() для
Гауссова источника =0.
для
Гауссова источника =0.
Оценка непрерывных параметров сигнала.
В большинстве случаев информация
передаётся путём модуляции какого-либо параметра ![]() по
закону передаваемого сообщения.
по
закону передаваемого сообщения.
В этом случае в приёмной части за
интервал наблюдения ![]() - этот параметр слабо
изменяется и его можно оценить, если параметр
- этот параметр слабо
изменяется и его можно оценить, если параметр ![]() будет
оценён по Т.Котельникова, то можно будет восстановить всю функцию.
будет
оценён по Т.Котельникова, то можно будет восстановить всю функцию.
![]()
Приём сигнала со случайной фазой.
Получим оптимальную процедуру сигнала со случайной фазой. Будем использовать логарифм соотношения правдоподобия для когерентных сигналов:
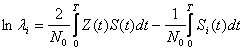
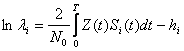 (3)
(3)
![]()
где ![]()
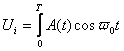
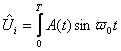
После подстановки получим:
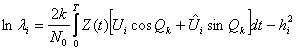
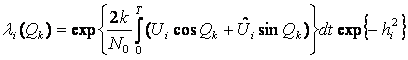 (1)
(1)
Т.к. ![]() - случайная
величина, то по случайной функции синтезировать не возможно, поэтому необходимо
найти
- случайная
величина, то по случайной функции синтезировать не возможно, поэтому необходимо
найти 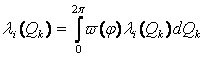 (2)
(2)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.