Виды уплотнения в многоканальных системах передачи, страница 7

  критерий Неймана-Пирсона

  критерий Вальда

Эти критерии нашли наиболее широкое применение.

Чем больше норма разности, тем легче сигналы различить в пространстве.

С геометрической точки зрения видно, что задача многостатистическая.

Если норма  меньше, то необходимо принимать гипотезу , а если больше чем , то принимаем гипотезу

     (1)

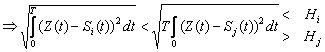     (2)

Возведём левую и правую часть в квадрат, к подынтегральным выражениям применим формулу квадратов разности, после преобразований получаем:

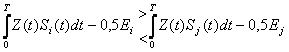  (3)   правило оптимальной процедуры

где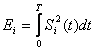

На основании полученной оптимальной процедуры можно обобщить структурную схему оптимального приёмника.

 

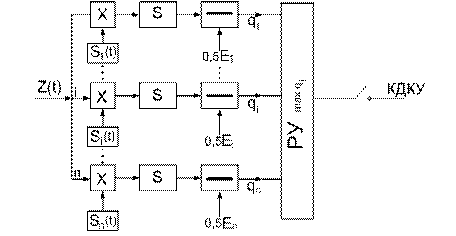
Наиболее широкое применение этот критерий нашёл в радиолокационных задачах.

Этот критерий так же является ассиметричным по отношению к начальным, в нём учитывается вероятность исхода, т.е. каждая ошибка неоднозначна.

Этот критерий схож с критерием минимального риска, где используется плата.

Считается крайне нежелательной ошибка типа ложной тревоги.

Рассмотрим на примере 2х альтернативной логики:

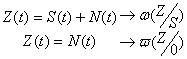
-вероятность ложной тревоги.

если

Вероятность  выбирается из тактических характеристик.

Критерий Вальда.

Суть состоит в выборе 2 порогов.

Критерий Котельникова.

Возникает вопрос, на основании чего ДМ должно принять одно из этих решений: .

Отсюда следует, что ДМ должно каким-либо способом для всех возможных гипотез  должно просчитать апостериорные вероятности.

Решающее устройство (ДМ) должно оценить эти характеристики однозначно связанные с этими апостериорными вероятностями и должно принять решение в пользу этой гипотезы, апостериорная вероятность которой максимальна и от сюда и название критерия:

Проанализируем (1) и распишем подробнее:

используя (1) запишем:

   (3)

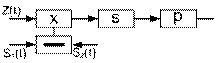
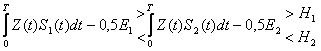
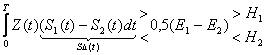
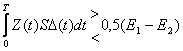
Соотношение сигнал/шум на выходе СФ.

СФ имеет структуру, которая согласуется со структурой сигнала.