Виды уплотнения в многоканальных системах передачи, страница 4

Энтропия зависимых источников .

6. Энтропия источника сообщений с независимыми элементами алфавита всегда больше источника с зависимыми элементами алфавита .

Функция - это импульсная характеристика идеального фильтра ФНЧ, в связи с тем, что на практике АЧХ идеального ФНЧ возникает инструментальная погрешность.

Возможна также инструментализация погрешности в результате того, что  неодинакова.

Теорема Котельникова для полосовых сигналов.

Полосовые сигналы это такие сигналы, энергия которых сосредоточена в узкой полосе частот.

На практике мы имеем дело с полосовыми сигналами:

Сигналы и помехи.

Помеха – это обычно сторонний элементарный сигнал, имеющий, туже природу (физическую).

Существует 2а типа:

- сигналы носители.

- сигналы сообщения.

сигналы в точке приёма всегда следует рассматривать как случайный процесс, обусловленный 2мя факторами:

• наличием помех.
• случайность самого сигнала сообщения.

Информационные характеристики сигналов.

Информация – это новые знания, приносимые сообщением об окружающем нас мире.

Мера измерения предъявляют 3и требования:

·  мера должна быть аддитивной

аддитивность означает симулирование информацией от разных источников.

·  мера должна быть универсальной

мера должна быть рассчитана на получение несколькими объектами.

·  мера должна отражать вероятностные характеристики.

Мера Хартли (1928)

Для оценки количества информации в непрерывных сообщениях используется и мера Шенона.

Для оценки  необходимо иметь статистические характеристики сигнала (Закон распределения информации).

                           

 Используемый шаг квантования   определяет точность сигнала.

Дифференциальная энтропия.

Найдём дифференциальную энтропию непрерывного сигнала.

 

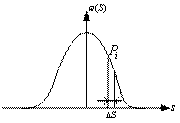
Дифференциальная энтропия является аддитивной мерой. Может принимать положительные и отрицательные значения.

Взаимная энтропия.

Взаимная энтропия – общее количество информации, которое содержит и один источник сообщения и второй источник в расчёте на одну букву алфавита.

Взаимную энтропию используют, как информационный критерий качества.

.

Свойства взаимной энтропии.

1.Взаимная энтропия   

, когда А и B – один источник, т.е.