Виды уплотнения в многоканальных системах передачи, страница 8

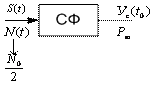
Задачу будем решать в частотной области.

 

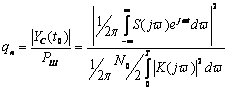
на входе

на выходе

Неравенство Коши-Бениковского

    

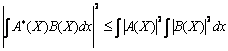
После подстановки этого равенства получим:

При введении 2х порогов пространство разбивается на 3и  области: , - область неопределённости.

Вероятность Л.Т.:

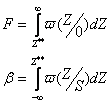
если

          

        

особенность 2х порогового критерия, что наблюдается явление случайной величиной.

-случайная величина, но - минимально возможное.

Синтез оптимальной процедуры точно

известного сигнала.

На основании статистического критерия можно получить оптимальную процедуру и на основании её построить схему, а затем определить высший предел помехоустойчивости.

Исходные данные:

- в канале действует аддитивный Гауссовский шум.

- задан вид модуляции.

- длительность сигнала одинакова и равна t (- техническая скорость).

Будем использовать критерий правдоподобия отношения, но т.к. длительность сигнала равна t, то ширина спектра и плотность распределения стремится к нулю.

Т.е.  и в этом пространстве записать данное отношение  к  не является возможным т.к. плотность .

Т.О. в начале необходимо ограничить ширину спектра:  и прейдём к n-мерному пространству.

меняться на и на выходе выявляется эффект обратной работы

Для решения проблемы обратной работы предложили использовать ОФМ

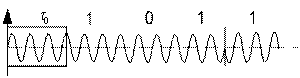
Схема преобразуется к виду:

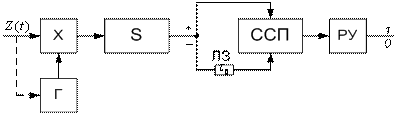
При таком приёме эффект обратной работы исключается, но платим за это:

а)

б)

Т.О. ,  но

Т.О. плата за устранение обратной работы является снижение помехоустойчивости в 2 раза.

       

Обеспечивает более высокую помехоустойчивость.

Потенциальная помехоустойчивость при