Применим закон распределения равновероятности:
![]()
![]() (4)
(4)
Подставляя (1) и (2) и (4) и вводя обозначения с фазой
![]()

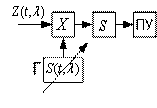
Последовательная схема может быть также реализована на основе СФ.
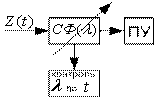
Нормальные и аномальные ошибки.
Необходимо рассматривать 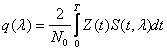
![]() ,
тогда
,
тогда
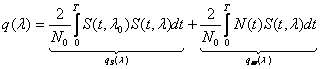
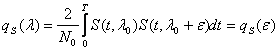
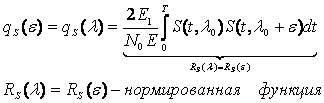
если ![]() ,
либо
,
либо ![]() соответствует
соответствует ![]() , то
, то![]()
![]()
Эта же задача стоит при радиоизмерениях. И она может решаться при построении оптимального устройства, с различными критериями.
Статистические критерии оценки непрерывных параметров
сигнала.
Cуществуют следующие критерии:
ü Критерий максимума функции правдоподобия.
ü
максимальная апостериорная плотность распределения вероятности
параметра ![]() .
.
ü Критерий минимума средне квадратичной ошибки.
ü Критерий Баеса.
Распишем каждый критерий более подробно.
Критерий максимального правдоподобия.
![]()
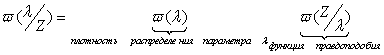
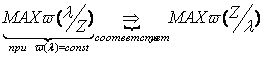 оценка
максимального правдоподобия.
оценка
максимального правдоподобия.
Критерий максимальной апостериорной вероятности.
Рассмотрим статистическую схему:

Оценивается значение максимального параметра.
Критерий минимальной средне квадратичной ошибки.
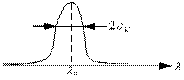
Ошибки, связанные с фиксацией ![]() , не выходящие за пределы
корреляционного пика называются нормальные ошибки (инстр. ошибки,
ошибки шума).
, не выходящие за пределы
корреляционного пика называются нормальные ошибки (инстр. ошибки,
ошибки шума).
Шумовая составляющая: 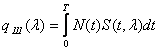
Дисперсия: ![]()
Шумовая составляющая имеет вид ![]() , но её особенность, что
количество сигнальных выбросов тем больше, чем больше шумовой уровень.
, но её особенность, что
количество сигнальных выбросов тем больше, чем больше шумовой уровень.
При регистрации шумовой выброс
может быть принят за сигнальный выброс. Ошибка может составить ![]() , а нормальные ошибки не выходят за
корреляционные пределы. Вероятность появления аномальных ошибок характеризует
неправильность измерения вообще.
, а нормальные ошибки не выходят за
корреляционные пределы. Вероятность появления аномальных ошибок характеризует
неправильность измерения вообще.
При проектировании задают соотношение сигнал/шум, чтобы избежать аномальных ошибок.
А среднеквадратичная ошибка
параметра ![]()
![]()
![]() .
.
![]() Расчёт среднеквадратической ошибки.
Расчёт среднеквадратической ошибки.
Рассмотрим формулу исходя из геометрического происхождения сигнала.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.