Технические характеристики:
Геометрическое взаимодействие сигнала и помехи.

![]()
![]() - эффективный радиус
гиперсферы. Если гиперсферу спроектировать на оси, мы получим дифференциальный
закон распределения.
- эффективный радиус
гиперсферы. Если гиперсферу спроектировать на оси, мы получим дифференциальный
закон распределения.
Синтез оптимальной процедуры приёма точного сигнала на основе геометрических
представлений.
Изобразим геометрическую задачу:
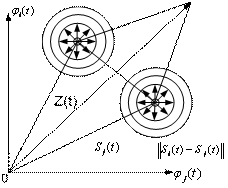
Будем считать, что сигналы с равной энергией.
![]()
Если норма разности: ![]()
![]() - нормированный.
- нормированный.
Любой сигнал в том или ином базисе может быть представлен в линейной комбинации базисных векторов.
Основные метрические соотношения в N-мерном пространстве.
Размерность пространства n определяется базой сигнала ![]()
![]() , где F
-ширина спектра.
, где F
-ширина спектра.
В n-мерном пространстве любой элемент представляется линейной комбинацией базисной функцией, т.е. его проекцией.
Если сигнал реальный, то обращается в бесконечномерное
пространство (пространство Гильберта, т.к. ![]() ).
).
Метрические соотношения:
1) ![]()
![]()
2)  - обобщенная теорема Пифагора
- обобщенная теорема Пифагора
3) 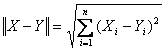 - норма разности
- норма разности
4) ![]() - равенство Коши-Бениковского
- равенство Коши-Бениковского
5) ![]() - скалярное произведение
- скалярное произведение
Метрические соотношения для бесконечного пространства
(пространство Гильберта).
Размерность сигнала определяется базой сигнала.
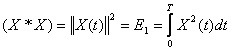 -
квадратурные нормы
-
квадратурные нормы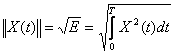 - Обобщённая теорема Пифагора для бесконечного пространства
- Обобщённая теорема Пифагора для бесконечного пространства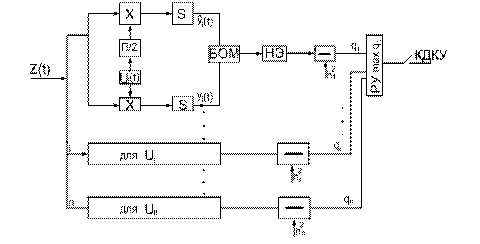
БОМ – блок определения модулей
НЭ – нелинейный элемент
Схема оптимальна для сигналов с равновероятным распределением фазы. Эта схема корреляционного типа, её так же можно изобразить в виде схемы согласованного фильтра.
Если сигналы с равной энергией, тогда нет необходимости в использовании вычитающих устройств и в использовании нелинейного элемента. Возможно сокращение каналов в зависимости от числа сигналов и их свойств.
Если плотность распределения фазы
будет любая, то оптимальная процедура будет определяться как: ![]() .
.
Статистические критерии качества приёма дискретных
сообщений.
Предложенный критерий Котельникова не является возможным применительно к радиотехническим задачам.
Чаще всего используются критерии:
![]() критерий Котельникова (критерий идеального наблюдателя, критерий
максимальной вероятности)
критерий Котельникова (критерий идеального наблюдателя, критерий
максимальной вероятности)
![]() критерий максимального среднего риска (Баесовый критерий)
критерий максимального среднего риска (Баесовый критерий)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.