Проверка основного уравнения динамики вращательного движения. Понятие о моменте инерции (Лабораторная работа № 7)

Лабораторная работа № 7

ПРОВЕРКА ОСНОВНОГО УРАВНЕНИЯ ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ. ПОНЯТИЕ О МОМЕНТЕ ИНЕРЦИИ

Цель работы: исследовать зависимость момента инерции системы от распределения масс относительно оси вращения и осуществить экспериментальную проверку основного уравнения динамики вращательного движения.

Приборы и принадлежности: установка FPM-06, набор грузов.

ТЕОРЕТИЧЕСКОЕ ОБОСНОВАНИЕ

          Основное уравнение динамики вращательного движения, описывающее вращения твердого тела вокруг неподвижной оси, имеет вид

,                                                         (7.1)

где  - суммарный момент внешних сил, действующих на тело,

I -момент инерции тела относительно оси вращения,

 -угловое ускорение тела.

          Записав векторное уравнение (7.1) в проекциях на ось вращения, нетрудно получить выражение для углового ускорения

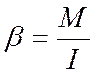                                                           (7.2)

Из (7.2) следует:

          а) при постоянном моменте инерции I угловое ускорение тела b прямо пропорционально действующему на него моменту внешних сил M:

 при I=const                                      (7.3)

          б) угловое ускорение b, сообщаемое телу постоянным моментом сил M, обратно пропорционально моменты инерции тела I:

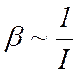 при M =const                                     (7.4)

Экспериментальную проверку следствий а) и б) можно осуществить с помощью маятника Обербека (см. Описание установки).

          Получим выражения (7.3) и (7.4) применительно к маятнику Обербека. Пренебрегая массой блока 7 (рисунок 1), массой нити 8, ее толщиной и силой трения о блок 7, запишем уравнения движения системы:

                                      (7.5)

                                             (7.6)

здесь m- масса грузов 10, - масса платформы на которой они расположены, T -проекция силы натяжения нити на направление движения грузов 10,  -проекция силы тяжести грузов 10 и платформы, a -ускорение грузов 10, r -радиус шкива 9,  -проекция момента силы трения в барабане 2 и блоке 9 на направление оси вращения, 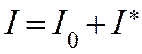 - момент инерции системы, который состоит из двух частей:  -момент инерции шкива 9 и стержней 1, который не изменяется во время опыта и  - момента инерции грузов 3 на стержнях 1, изменяющийся при изменении их числа и положения относительно оси вращения.

          Определив из уравнения (7.5) значение T и подставив его в (6) находим

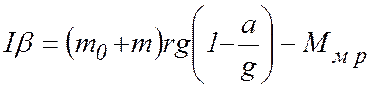                             (7.7)

Учитывая, что 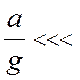 1 и пренебрегая моментом сил трения 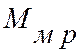 из (7.7) имеем

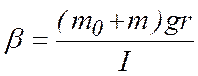                                            (7.8)

Если грузы 10 опускаются за время t с высоты h, то ускорение их движения 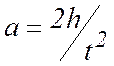. Таким же будет и ускорение любой точки на поверхности шкива 9, вращающегося с угловым ускорением . Следовательно

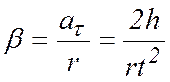                                                (7.9)

Подставив (9) в (8) и решив полученное уравнение относительно 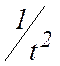, приходим к соотношению

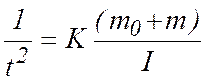                                           (7.10)

в котором постоянство величины 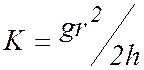 обеспечивается неизменностью величин r и h на протяжении опыта.

          Согласно (7.10), справедливость следствия a) может быть установлен по характеру зависимости величин 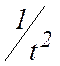 от m, определяемой экспериментально при условии.

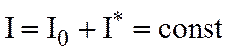          Потребовав постоянства массы m грузов 10 на протяжении опыта, что эквивалентно условию M =const, сведем проверку следствия б) к определению характера зависимости величины 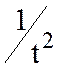 от .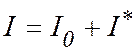

          Практически более удобно исследовать характер обратной зависимости, т.е. зависимости величины  от I, которая, согласно (10), является линейной

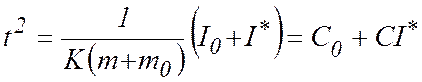                      (7.11)

Момент инерции  можно изменить либо меняя число грузов 3 на стержнях 1 (рисунок 1), либо изменяя их положение относительно оси вращения. Так как в работе используется вторая возможность, то удобно принять момент инерции  грузов 3, расположенных на стержнях 1 на расстоянии R=l от центра вращения, за 1 условную единицу. Поскольку

,                                                        (7.12)

то момент инерции  при увеличении расстояния R в два (R=2l), три (R=3l) и т.д. раз, соответственно равен 4, 9 и т.д. условным единицам. Справедливость утверждения (7.12) проверяется в первом упражнении. Получим формулу удобную для его экспериментальной проверки.

          При  (грузов 3 на стержнях нет), из (7.7), при учете сделанных приближений следует, что момент инерции  шкива 9 и стержней 1 относительно оси вращения, равен