ТЕМА 9 РАБОТА И ЭНЕРГИЯ
1 Работа, мощность.
2 Консервативные и диссипативные силы.
3 Кинетическая и потенциальная энергия механической системы.
4 Закон сохранения энергии.
Вопросы для самоподготовки
1 Напишите различные возможные варианты выражения для работы. Поясните смысл величин входящих в эти выражения.
2 В каких единицах измеряются работа и мощность в
системе СИ? Дайте определения этих единиц. ![]() это
единица измерения работы или мощности?
это
единица измерения работы или мощности?
3 Сформулируйте теорему об изменении кинетической энергии.
4 Частица движется равномерно по окружности. Чему равна работа равнодействующей всех сил, действующих на частицу: а) за один оборот, б) за половину оборота, в) за четверть оборота?
5 Какие силы называют консервативными? диссипативными? Приведите примеры консервативных и диссипативных сил.
6 Дайте определение потенциальной энергии. Чем она обусловлена?
7 Почему потенциальная энергия может быть определена только с точностью до некоторой постоянной? Что это за постоянная?
8 Как следует понимать выражение «Потенциальная энергия является функцией состояния системы»?
9 Сформулируйте закон сохранения энергии. Почему в механике рассматривают только два вида энергии - кинетическую и потенциальную?
10 Приведите пример замкнутой механической системы, в которой закон сохранения механической энергии не выполняется.
Основные понятия по теме
Пусть под действием силы ![]() материальная
точка совершает малое перемещение
материальная
точка совершает малое перемещение ![]() . Действие силы
. Действие силы ![]() на перемещении
на перемещении ![]() характеризуют
величиной
характеризуют
величиной ![]() , равной скалярному произведению этих
векторов, которое называется элементарной работой силы
, равной скалярному произведению этих
векторов, которое называется элементарной работой силы ![]() на перемещении
на перемещении ![]() :
:
![]() . (9.1)
. (9.1)
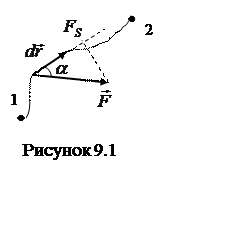
Здесь ![]() угол между векторами
угол между векторами ![]() и
и ![]() ,
, ![]() элементарный путь,
элементарный путь, ![]() проекция
вектора
проекция
вектора ![]() на вектор
на вектор ![]() (рисунок
9.1). Требование малости перемещения
(рисунок
9.1). Требование малости перемещения ![]() означает, что модуль
вектора силы и угол
означает, что модуль
вектора силы и угол ![]() в пределах этого перемещения не
изменяются.
в пределах этого перемещения не
изменяются.
В общем случае работа силы ![]() на
участке траектории от точки 1 до точки 2 равна алгебраической сумме
элементарных работ на отдельных бесконечно малых участках пути
на
участке траектории от точки 1 до точки 2 равна алгебраической сумме
элементарных работ на отдельных бесконечно малых участках пути
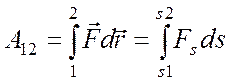 . (9.2)
. (9.2)
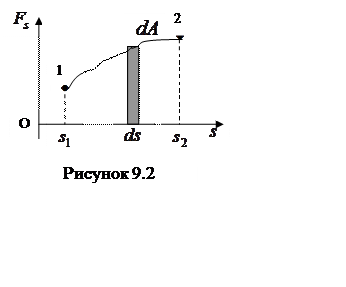
Выражение (9.2) имеет наглядный
геометрический смысл. Если зависимость ![]() от
от ![]() задана графически, то работа
задана графически, то работа ![]() определяется площадью соответствующей
криволинейной трапеции (рисунок 9.2).
определяется площадью соответствующей
криволинейной трапеции (рисунок 9.2).
Для характеристики скорости, с которой совершается
работа, вводят понятие мощности. Мощность ![]() силы
силы ![]() - это работа, совершаемая силой
- это работа, совершаемая силой ![]() за единицу времени
за единицу времени
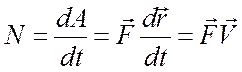 .
(9.3)
.
(9.3)
Таким образом, мощность, развиваемая силой ![]() , равна скалярному произведению вектора
силы на вектор скорости, с которой движется точка приложения силы.
, равна скалярному произведению вектора
силы на вектор скорости, с которой движется точка приложения силы.
Вычисление работы конкретных сил по формуле (9.2) показывает, что работа некоторых из них не зависит от формы траектории и определяется только начальным 1 и конечным 2 положениями точки. Силы, обладающие таким свойством, называются консервативными. Примерами таких сил могут служить:
- сила тяжести ![]()
![]() ;
(9.4)
;
(9.4)
- сила упругости ![]()
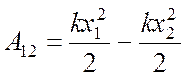 .
(9.5)
.
(9.5)
Очевидно, что работа консервативных сил на любом замкнутом пути равна нулю.
Все силы, не являющиеся консервативными, называются неконсервативными. Важным примером неконсервативных сил могут служить диссипативные силы, к которым относятся силы трения и сопротивления. Работа этих сил зависит от пути между начальным и конечным положениями точки и не равна нулю на любом замкнутом пути.
Независимость работы консервативных сил от пути между точками 1 и 2 позволяет ввести для этих сил понятие потенциальной энергии.
Потенциальной энергией тела в состоянии 1 называют величину равную работе по перемещению тела из этого состояния в «бесконечность» под действием только консервативных сил
![]() .
(9.6)
.
(9.6)
Термин «бесконечность» в данном определении имеет условный смысл. Им обозначено состояние тела в котором его потенциальная энергия принята равной нулю.
Вычислим работу, совершаемую при перемещении тела из состояния 1 в состояние 2 (рисунок 9.3). Учитывая тот факт, что работа консервативных сил не зависит от пути, получаем
![]() . (9.7)
. (9.7)
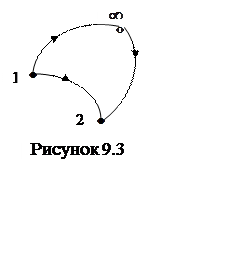 Из выражения
(9.7) следует, что работа при перемещении тела из состояния 1 в состояние 2
равна убыли потенциальной энергии тела.
Из выражения
(9.7) следует, что работа при перемещении тела из состояния 1 в состояние 2
равна убыли потенциальной энергии тела.
Приведенная выше формулировка (9.6) определяет потенциальную энергию тела в поле консервативных сил. При этом сила и потенциальная энергия связаны соотношением
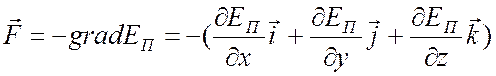 . (9.8)
. (9.8)
Потенциальная энергия взаимодействующих тел определяется их взаимным расположением и характером сил взаимодействия между ними.
Помимо потенциальной энергии в механике рассматривается кинетическая энергия. Кинетическая энергия – это энергия движения тела. Она зависит только от массы и скорости тела. Для точечного тела
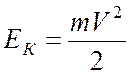 .
(9.9)
.
(9.9)
Связь кинетической энергии и работы устанавливает теорема
об изменении кинетической энергии: изменение кинетической
энергии тела при его перемещении из состояния 1 в состояние 2 равно работе всех
сил приложенных к телу на этом перемещении ![]()
![]() .
(9.10)
.
(9.10)
Сумму кинетической и потенциальной энергий называют полной механической энергией
![]() .
(9.11)
.
(9.11)
Записав выражения аналогичные (9.7) и (9.10) для системы тел, нетрудно получить, что для произвольно выбранных состояний 1 и 2
![]() .
(9.12)
.
(9.12)
Соотношение (9.12) выражает закон сохранения энергии: в системе тел, между которыми действуют только консервативные силы, полная механическая энергия не изменяется
![]() .
(9.13)
.
(9.13)
Закон сохранения энергии является следствием однородности времени – инвариантности физических законов относительно выбора начала отсчета времени.
Примеры решения задач
 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.