Тема 10Столкновение тел
1 Основная задача теории столкновений
2 Удары и их классификация
3 Коэффициенты восстановления
4 Векторная диаграмма импульсов
Основные понятия по теме
Вопросы для самоподготовки
1 Сформулируйте основную задачу теории столкновений тел. Какие приближения используются при решении этой задачи?
2 Что понимают под внутренней энергией при столкновении тел?
3 Что такое удар? В каких случаях удар называют абсолютно неупругим, неупругим, упругим?
4 Какие удары называют центральными?, косыми?
5 Дайте определения коэффициентов восстановления по скорости и по энергии. В каких пределах они могут изменяться?
6 Опишите качественно поведение двух сталкивающихся шаров, один из которых первоначально покоился, в случае центрального упругого удара в зависимости от соотношения их масс.
7 Какими факторами определяется величина переданной при упругом столкновении энергии от движущейся частицы к мишени? При каком условии переданная энергия будет максимальной?
8 Как строиться векторная диаграмма импульсов? Какие вопросы она позволяет решать?
9 Когда падающая на мишень частица в результате упругого столкновения не может отклониться на любой угол и когда может?
10 Что такое предельный угол отклонения? В каких случаях он существует? Чему он равен?
Примеры решения задач
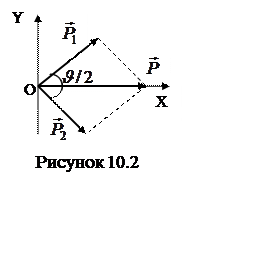 1 После упругого соударения тела массы
1 После упругого соударения тела массы ![]() , двигавшегося поступательно, с покоившимся
телом массы
, двигавшегося поступательно, с покоившимся
телом массы ![]() оба тела разлетаются симметрично
относительно направления вектора скорости первого тела до удара (рисунок 10.2).
Определить при каких значениях
оба тела разлетаются симметрично
относительно направления вектора скорости первого тела до удара (рисунок 10.2).
Определить при каких значениях ![]()
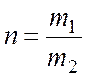 это
это
возможно.
Рассчитать ![]() для двух случаев: угол
для двух случаев: угол ![]() между векторами скоростей тел после удара
равен
между векторами скоростей тел после удара
равен ![]() и
и ![]() .
.
Решение. При упругом ударе выполняются закон сохранения импульса
![]() (1)
(1)
и закон сохранения энергии
![]() (2)
(2)
Записав векторное уравнение (1) в проекциях на оси Х и Y выбранной системы координат и учитывая выражения для импульса и кинетической энергии, перепишем (1) и (2) в виде системы скалярных уравнений
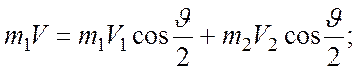
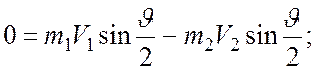
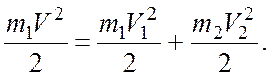
Записанная система легко преобразуется к виду
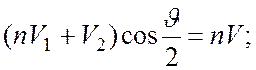 (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
Здесь
![]() искомое отношение масс. Для определения
искомое отношение масс. Для определения ![]() подставим
подставим ![]() в первое и третье уравнения системы уравнений (
в первое и третье уравнения системы уравнений (![]() ). В результате имеем
). В результате имеем
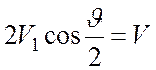 и
и ![]() .
.
Отсюда,
исключая скорости, находим ![]()
При ![]()
![]() то есть этот случай возможен если массы
тел одинаковы. Если
то есть этот случай возможен если массы
тел одинаковы. Если ![]() то
то ![]() Следовательно,
этот случай реализуется при условии
Следовательно,
этот случай реализуется при условии ![]()
2 Два
одинаковых шара претерпевают центральный удар. До удара второй шар неподвижен,
а первый движется со скоростью ![]() Характер удара шаров
таков, что потеря механической энергии системы составляет ровно одну треть той
потери, которая имела бы место при абсолютно неупругом ударе этих же шаров.
Найти скорости шаров
Характер удара шаров
таков, что потеря механической энергии системы составляет ровно одну треть той
потери, которая имела бы место при абсолютно неупругом ударе этих же шаров.
Найти скорости шаров ![]() и
и ![]() после
удара.
после
удара.
Решение. Рассматриваемый удар является неупругим. Следовательно, в результате удара часть механической энергии системы переходит во внутреннюю энергию сталкивающихся шаров. Потеря энергии при абсолютно неупругом ударе двух шаров, один из которых покоился,
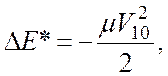
где
![]() приведенная масса. При
приведенная масса. При ![]()
![]() и
и ![]() Здесь
Здесь ![]() масса
одного шара.
масса
одного шара.
Потеря энергии для данного удара, согласно условию задачи,
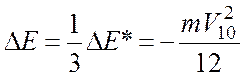 .
(1)
.
(1)
С другой стороны
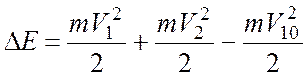 .
(2)
.
(2)
Приравняв правые части (1) и (2), приходим к уравнению
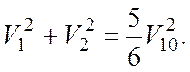 (3)
(3)
Учитывая равенство масс шаров, из закона сохранения импульса получаем
![]() (4)
(4)
Теперь, для определения искомых скоростей, достаточно
решить систему состоящую из уравнений (3) и (4). Так как ![]() то для нахождения
то для нахождения ![]() получаем
квадратное уравнение
получаем
квадратное уравнение
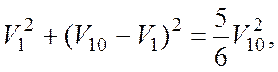
корни которого
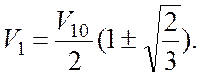
Поскольку скорость первого шара после удара увеличиться не может, то из двух найденных решений следует сохранить только решение со знаком «минус» в круглых скобках. Следовательно, скорости шаров после удара
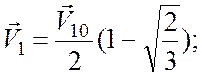
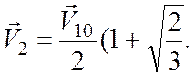 ).
).
Задачи
1 Шар 1
массой ![]() движущийся со скоростью
движущийся со скоростью ![]() , сталкивается с шаром 2, масса которого
, сталкивается с шаром 2, масса которого ![]() <
<![]() и
скорость
и
скорость ![]() >
>![]() Считая
удар центральным и упругим, найти скорости шаров после удара в двух случаях: 1)
малый шар нагоняет большой шар, движущийся в том же направлении; 2) шары
движутся навстречу друг другу.
Считая
удар центральным и упругим, найти скорости шаров после удара в двух случаях: 1)
малый шар нагоняет большой шар, движущийся в том же направлении; 2) шары
движутся навстречу друг другу.
2 Рассчитайте
коэффициенты восстановления по скорости ![]() и по
энергии
и по
энергии ![]() для удара рассмотренного в примере 2.
Сравните результаты с соответствующими выражениями для упругого и абсолютно
неупругого ударов.
для удара рассмотренного в примере 2.
Сравните результаты с соответствующими выражениями для упругого и абсолютно
неупругого ударов.
3 Частица 1,
имеющая скорость ![]() испытала лобовое столкновение с
покоящейся частицей 2 такой же массы. В результате столкновения кинетическая
энергия системы уменьшилась на
испытала лобовое столкновение с
покоящейся частицей 2 такой же массы. В результате столкновения кинетическая
энергия системы уменьшилась на ![]() Найти модуль и
направление скорости частицы 1 после столкновения.
Найти модуль и
направление скорости частицы 1 после столкновения.
4 Докажите,
что в случае косого удара двух одинаковых шаров, один из которых первоначально
покоился, угол разлета всегда равен ![]() Проиллюстрируйте
результат используя векторную диаграмму импульсов.
Проиллюстрируйте
результат используя векторную диаграмму импульсов.
5 Два
одинаковых шара движутся со скоростями ![]() и
и ![]() так, что угол между направлениями их
движения равен
так, что угол между направлениями их
движения равен ![]() . После упругого столкновения
скорости шаров оказались равными
. После упругого столкновения
скорости шаров оказались равными ![]() и
и ![]() Найти угол
Найти угол ![]() между
направлениями их разлета после столкновения.
между
направлениями их разлета после столкновения.
6 В
результате упругого центрального удара шара 1 массы ![]() с
покоившимся шаром 2 оба шара разлетелись в противоположных направлениях с
одинаковыми скоростями. Найти массу шара 2.
с
покоившимся шаром 2 оба шара разлетелись в противоположных направлениях с
одинаковыми скоростями. Найти массу шара 2.
 7 Движущийся шар 1 массы
7 Движущийся шар 1 массы ![]() ударяется
о неподвижный шар 2 массы
ударяется
о неподвижный шар 2 массы ![]() . После упругого удара
шары 1 и 2 летят в направлениях, образующих соответственно углы
. После упругого удара
шары 1 и 2 летят в направлениях, образующих соответственно углы ![]() и
и ![]() с
начальным направлением движения шара 1 (рисунок 10.3).
с
начальным направлением движения шара 1 (рисунок 10.3).
1.
Найти, при каком соотношении масс ![]() и
и ![]() возможны
случаи: а)
возможны
случаи: а) ![]() б)
б) ![]() в)
в) ![]() г)
г) ![]()
2. Для случаев указанных в пункте 1 построить векторные диаграммы импульсов.
3.
Чему равно при![]() предельно возможное значение угла
предельно возможное значение угла ![]()
4.
Возможен ли случай ![]()
8 Для столкновения шаров, описанного в задаче 7, найти:
1. Какую часть ![]() своей
кинетической энергии передает первый шар второму в случаях: а)
своей
кинетической энергии передает первый шар второму в случаях: а) ![]() б)
б) ![]() в)
в) ![]() г)
г) ![]()
2. Чему равно предельное значение ![]() в случае 1б)?
в случае 1б)?
3. При каком соотношении масс ![]() и
и
![]() в случаях 1в) и 1г) потери энергии
максимальны?
в случаях 1в) и 1г) потери энергии
максимальны?
9 Какую
часть ![]() своей кинетической энергии теряет частица
массы
своей кинетической энергии теряет частица
массы ![]() при упругом рассеянии под предельным углом
на покоящейся частице массы
при упругом рассеянии под предельным углом
на покоящейся частице массы ![]()
10 Частица 1
массы ![]() испытала столкновение с покоившейся
частицей 2 массы
испытала столкновение с покоившейся
частицей 2 массы ![]() , в результате которого частица 1
отклонилась на угол
, в результате которого частица 1
отклонилась на угол ![]() /2, а частица 2 отскочила под
углом
/2, а частица 2 отскочила под
углом ![]() к первоначальному направлению движения
частицы 1. На сколько процентов и как изменилась кинетическая энергия этой
системы после столкновения, если
к первоначальному направлению движения
частицы 1. На сколько процентов и как изменилась кинетическая энергия этой
системы после столкновения, если ![]()
Ответы и указания
1 1) 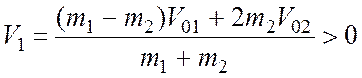 , то есть шар 1 будет двигаться в том же
направлении, что и до столкновения;
, то есть шар 1 будет двигаться в том же
направлении, что и до столкновения; 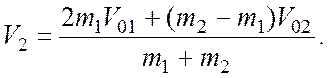
2) 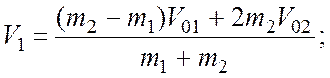
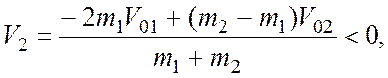 то есть меньший шар будет двигаться в
направлении противоположном первоначальному.
то есть меньший шар будет двигаться в
направлении противоположном первоначальному.
2 ![]()
![]()
![]()
3 Будет
двигаться в том же направлении со скоростью ![]() При
При ![]() скорость
скорость ![]()
5 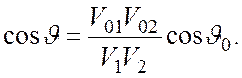
6 ![]()
7 1.а)![]() б)
б)![]() в)
в)![]() г)
г)![]() .
.
2) см. рисунок 3.
3)
![]()
4) невозможен.
8 1.а)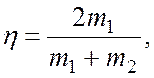 б)
б)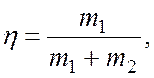 в) г)
в) г)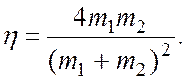
2).![]()
3).![]()
9 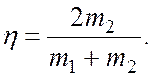 Указание: используйте векторную
диаграмму импульсов.
Указание: используйте векторную
диаграмму импульсов.
10 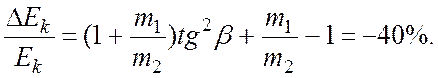
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.