Волны в упругой среде. Энергия упругой волны. Стоячие волны. Эффект Доплера

Тема 18Волны в упругой среде

1

2 Энергия упругой волны

3 Стоячие волны

4 Эффект Доплера

Основные понятия по теме

Упругой волной называется процесс распространения колебаний частиц в упругой среде. Если в такой среде каким-либо способом вызвать колебания одной ее точки, то в результате упругих взаимодействий в среде возникнет бегущая волна, которая в процессе своего распространения будет заставлять совершать колебания все новые и новые частицы среды. Граница, отделяющая область среды в которой возникли колебания частиц от области, в которой частицы еще не начали колебаться, называется фронтом волны. В зависимости от формы фронта волны принято говорить о плоских, сферических и др. волнах.

Наряду с фронтом волны, при описании волн, используется другой геометрический образ ‒ волновая поверхность. Волновой поверхностью называют геометрическое место точек среды колеблющихся в одинаковой фазе. Из этого определения ясно, что фронт волны представляет собой волновую поверхность максимально удаленную от источника колебаний. Направление, в котором распространяется волна, называют лучом.

В зависимости от направления колебаний частиц среды относительно направления распространения волны различают два вида волн: продольные и поперечные. В продольной волне частицы смещаются вдоль направления распространения волны. В поперечной волне смещение частиц перпендикулярно направлению распространения волны. Продольные и поперечные волны могут возникать в твердых телах. В жидкостях и газах, в связи с отсутствием в них деформаций сдвига, могут существовать только продольные волны.

Так как волна, по своей сути, представляет собой колебания «отпущенные на свободу», то для ее описания пользуются теми же величинами, что и для колебаний, добавляя к ним скорость распространения V и порождаемое ее понятие длины волны. Длиной волны называют расстояние проходимое волной за время одного полного колебания, то есть за период:

.                                           (18.1)

Длине волны можно дать и другое определение: длина волны ‒ это наименьшее расстояние между двумя точками, колеблющимися в одинаковой фазе.

Простейшей волной распространяющейся в направлении оси Х является бегущая волна, уравнение которой

.                             (18.2)

Здесь смещение частицы с координатой х в момент времени t, волновое число, показывающее сколько длин волн  укладывается на отрезке длиной  метров, частота волны.

В случае плоской волны распространяющейся в направлении нормали  к ее фронту, уравнение (18.2) принимает вид

,                               (18.3)

где радиус-вектор частицы среды, волновой вектор.

Непосредственной подстановкой нетрудно убедиться, что выражение (18.3) является решением уравнения

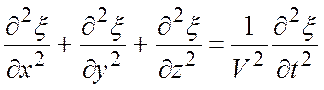,                          (18.4)

если

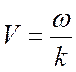.                                             (18.5)

Уравнение (18.4) носит название волнового уравнения.

Скорость , определяемая формулой (18.5), является фазовой скоростью волны. В упругой среде с плотностью  

 в случае продольных и  в случае поперечных волн, где Е и модуль Юнга и модуль сдвига среды соответственно.

Распространение волны в упругой среде сопровождается колебаниями частиц среды и ее деформациями. Следовательно, среда получает дополнительный запас энергии от источника колебаний. Для бегущей волны (18.2) мгновенная плотность энергии, то есть энергия приходящаяся в данный момент времени на единицу объема среды,

.                           (18.6)

Соответственно, среднее за период значение плотности энергии равно

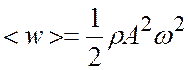.                                   (18.7)

Из (18.6) видно, что мгновенная плотность энергии в различных точках среды различна. Кроме того, плотность энергии в одной и той же точке среды в разные моменты времени так же различна, что свидетельствует о переносе энергии волной.

Для описания переноса энергии вводят понятие о потоке энергии.

Под потоком энергии Ф понимают количество энергии переносимое волной за единицу времени через определенную поверхность S.

Поток энергии через единичную площадку, перпендикулярную к направлению переноса энергии, называется плотностью потока энергии:

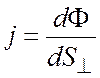.                                              (18.8)

Для определения плотности потока энергии и его направления вводят вектор Умова. Для бегущей волны вектор Умова

,                                                (18.9)

где плотность энергии, вектор скорости, нормальный к волновой поверхности в данной точке площадки S.

С учетом (18.7), для среднего за период значения вектора Умова можем записать

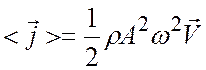.                                    (18.10)

Это выражение справедливо не только для плоских волн, но и для волн любого вида.

При распространении в упругой среде одновременно нескольких волн происходит их наложение друг на друга. Процесс наложения волн подчиняется принципу суперпозиции. Согласно принципу суперпозиции налагающиеся волны не оказывают взаимного влияния друг на друга, то есть каждая волна распространяется так, как будто другие отсутствуют. Это означает, что колебания частиц среды, находящихся в области наложения волн, являются векторной суммой колебаний, которые совершали бы частицы при распространении каждой из волн в отдельности.

При наложении двух плоских волн имеющих одинаковые частоты и амплитуды и распространяющихся в противоположных направлениях

  и 

результирующее смещение  частицы среды с координатой х в момент времени  равно сумме смещений  и :