Движение тел переменной массы. Уравнение Мещерского. Реактивная сила. Формула Циолковского

ТЕМА 8 ДВИЖЕНИЕ ТЕЛ ПЕРЕМЕННОЙ МАССЫ

1 Уравнение Мещерского.

2 Реактивная сила.

3 Формула Циолковского.

Вопросы для самоподготовки

1 Напишите уравнение движения тела переменной массы: а)в общем случае; б)для случая отделения частиц от основного тела; в)для случая присоединения частиц.

2 Какие частные случаи приводят к упрощению уравнения Мещерского?

3 Какая сила называется реактивной? Поясните на простом примере, как возникает реактивная сила.

4 Напишите формулу для реактивной силы, обусловленной: а)отделением частиц; б)присоединением; в)одновременным присоединением и отделением частиц. Рассмотрите вопрос о направлении реактивной силы в указанных случаях.

5 Будет ли увеличиваться скорость ракеты, если скорость истекающих газов относительно Земли меньше скорости самой ракеты и вытекающие из сопла газы летят вслед за ракетой?

Основные понятия по теме

Из основного уравнения динамики (     ) следует, что изменение импульса тела может быть обусловлено как изменением его скорости, так и изменением массы тела. Если масса тела изменяется со скоростью dm/dt, то уравнение поступательного движения твердого тела имеет вид

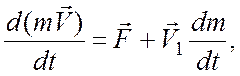                                              (8.1)

где равнодействующая внешних сил, приложенных к телу; скорость присоединяющейся массы до присоединения (если  или скорость отделяющейся массы после отделения (если .

Вычислив производную в левой части уравнения (8.1), получаем

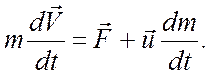                                               (8.2)

Уравнение (8.2) называется уравнением Мещерского. Здесь  скорость присоединяющейся или отделяющейся массы относительно движущегося тела. Слагаемое

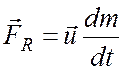                                                      (8.3)

в уравнении (8.2) определяет реактивную силу.

Примеры решения задач

1 Автоматическая станция совершила мягкую посадку на поверхность Луны. Масса станции после выведения на траекторию полета к Луне была равна  За время  до посадки станции была включена тормозная двигательная установка. Система управления посадкой обеспечила гашение скорости с  до нуля у поверхности Луны. Масса топлива составляла половину массы станции перед ее торможением, и можно считать, что оно израсходовано полностью. Какая реактивная сила действовала на станцию при посадке? Силу тяготения не учитывать.

Решение. Требование отсутствия сил тяготения означает, что в процессе торможения внешние силы на станцию не действуют. Следовательно, уравнение движения станции (уравнение Мещерского) имеет вид

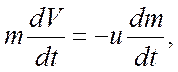                                                           (1)

где  масса станции с топливом в момент времени t после начала торможения, ее скорость, скорость выбрасываемых газов относительно станции.

Реактивная сила торможения, всегда направленная навстречу скорости u, равна

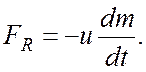                                                               (2)

Напомним, что при посадке станции тормозные двигатели выбрасывают струю газа по направлению движения.

Определим скорость истечения газов u. Для этого разделим переменные в уравнении (1) и проинтегрируем обе части полученного выражения с учетом заданных условий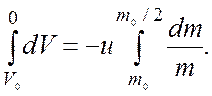 Отсюда

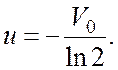                                                                (3)

Аналогично, разделив переменные в уравнении (2) и интегрируя обе части 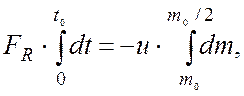  легко найти

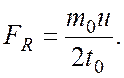                                                                (4)

Из (4), с учетом (3), окончательно получаем

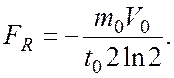                                                           (5)

Знак «минус» означает, что сила торможения противоположна направлению скорости станции  Вычисления по формуле (5) дают

2 Ракета поддерживается в воздухе на постоянной высоте, выбрасывая вертикально вниз струю газа со скоростью  Сколько времени ракета может оставаться в состоянии покоя, если начальная масса топлива составляет  от ее массы без топлива?