Тема 12 Динамика твердого тела
1 Основное уравнение динамики вращательного движения
2 Момент инерции
3 Вращение твердого тела вокруг неподвижной оси
4 Плоское движение твердого тела
Основные понятия по теме
К основным видам движения твердого тела относятся:
- поступательное движение твердого тела;
- вращение твердого тела вокруг неподвижной оси;
- плоское движение твердого тела;
- вращение твердого тела вокруг неподвижной точки;
- свободное движение твердого тела.
Из перечисленных видов движения четыре последних типа связаны с вращательным движением. При описании этих видов движения используется уравнение моментов
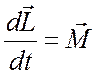 ,
(12.1)
,
(12.1)
которое принято называть основным уравнением динамики вращательного движения. Так же как и основное уравнение динамики основное уравнение динамики вращательного движения (12.1) можно записать в другом виде
![]() ,
(12.2)
,
(12.2)
где
![]() угловое ускорение тела.
угловое ускорение тела.
Величина ![]() , входящая в уравнение
(12.2), является аналогом массы при вращательном движении твердого тела. Ее
называют момент инерции. Момент инерции материальной точки равен
, входящая в уравнение
(12.2), является аналогом массы при вращательном движении твердого тела. Ее
называют момент инерции. Момент инерции материальной точки равен
![]() ,
(12.3)
,
(12.3)
где
![]() масса материальной точки,
масса материальной точки, ![]() расстояние от материальной точки до оси
вращения. Для системы материальных точек и твердого тела моменты инерции
соответственно равны
расстояние от материальной точки до оси
вращения. Для системы материальных точек и твердого тела моменты инерции
соответственно равны
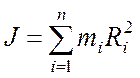 ;
(12.4)
;
(12.4)
![]()
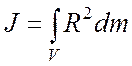 .
(12.5)
.
(12.5)
В выражении (12.5) интегрирование ведется по объему тела.
Момент инерции зависит от положения оси вращения и распределения масс относительно этой оси. Приведем выражения для моментов инерции некоторых тел относительно оси вращения,.положение которой указывается в скобках.
Сплошной цилиндр или диск радиуса R(ось симметрии)
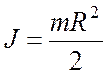 . (12.6)
. (12.6)
Полый тонкостенный цилиндр радиуса R или обруч (ось симметрии)
![]() .
(12.7)
.
(12.7)
Однородный тонкий стержень длиной l (ось перпендикулярна стержню и проходит через его середину)
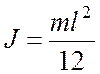 .
(12.8)
.
(12.8)
Шар радиуса R (ось проходит через центр шара)
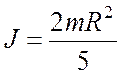 .
(12.9)
.
(12.9)
Если известен момент инерции тела относительно оси, проходящей через его центр масс С, то момент инерции относительно любой другой параллельной оси определяется теоремой Штейнера:
момент инерции тела J
относительно произвольной оси Z равен сумме момента инерции тела ![]() относительно параллельной оси, проходящей
через центр масс С тела, и произведения массы m тела на
квадрат расстояния а между осями.
относительно параллельной оси, проходящей
через центр масс С тела, и произведения массы m тела на
квадрат расстояния а между осями.
Вращающееся тело, как и тело движущееся поступательно, обладает энергией движения.
Кинетическая энергия твердого тела вращающегося вокруг
неподвижной оси Z с угловой скоростью ![]()
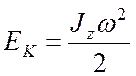 .
(12.10)
.
(12.10)
Кинетическая энергия тела совершающего плоское движение равна
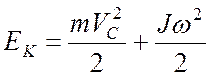 , (12.11)
, (12.11)
где
![]() скорость центра масс тела,
скорость центра масс тела, ![]() угловая скорость тела,
угловая скорость тела, ![]() момент инерции тела относительно
собственной оси.
момент инерции тела относительно
собственной оси.
Вопросы для самоконтроля
1 Назовите виды движения твердого тела.
2 Что понимают под плоским движением твердого тела? Приведите примеры такого движения. Почему этот вид движения называют плоское движение?
3 Чем отличаются траектории точки твердого тела вращающегося вокруг неподвижной оси и вокруг неподвижной точки О?
4 Дайте определение момента инерции материальной точки, системы материальных точек, твердого тела. Что характеризует момент инерции? От каких факторов он зависит?
5 Объясните смысл утверждения «момент инерции это аддитивная величина».
6 Сформулируйте теорему Штейнера.
7 Что понимаю под тензором моментов инерции? Чем обусловлено необходимость введения такого понятия? Какие моменты инерции называются осевыми?, центробежными?
8 Запишите основное уравнение динамики вращательного движения в различных формах. Установите аналогию записанных выражений с уравнениями динамики поступательного движения.
9 Опишите последовательность действий при решении основной задачи динамики твердого тела.
10 Запишите выражения для энергии твердого тела вращающегося вокруг неподвижной оси, вокруг неподвижной точки. Напишите аналогичное выражение для тела, совершающего плоское движение.
Примеры решения задач
1 В схеме,
показанной на рисунке 12.1, определить ускорение груза массы m.
Масса М, момент инерции J, внутренний ![]() и внешний
и внешний ![]() радиусы
ступенчатого блока известны.
радиусы
ступенчатого блока известны.
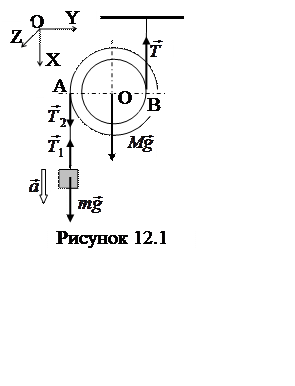 Решение. Силы, действующие на груз и блок, показаны на рисунке
12.1. Запишем второй закон Ньютона для груза m
Решение. Силы, действующие на груз и блок, показаны на рисунке
12.1. Запишем второй закон Ньютона для груза m
![]() . (1)
. (1)
Для блока, который участвует в поступательном и вращательном движениях, необходимо записать второй закон Ньютона и основное уравнение динамики вращательного движения
![]() ;
(2)
;
(2)
![]() . (3)
. (3)
В
уравнении (3) через ![]() обозначен момент,
соответствующий силе
обозначен момент,
соответствующий силе ![]() относительно точки О лежащей на
оси блока.
относительно точки О лежащей на
оси блока.
В проекциях на оси системы координат XYZ система
векторных уравнений (![]() ) принимает вид
) принимает вид
![]() ;
(4)
;
(4)
![]() ;
(5)
;
(5)
![]() (6)
(6)
и
содержит шесть неизвестных: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Для решения системы уравнений (![]() )
учтем, что, согласно третьему закону Ньютона
)
учтем, что, согласно третьему закону Ньютона ![]() . Кроме
того, для точки A, участвующей в поступательном движении груза m и вращательном
движении блока, и точки В, участвующей в поступательном и вращательном
движениях блока, можем записать
. Кроме
того, для точки A, участвующей в поступательном движении груза m и вращательном
движении блока, и точки В, участвующей в поступательном и вращательном
движениях блока, можем записать
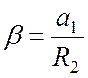 и
и 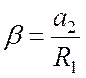 .
.
Учитывая приведенные выше соотношения, вместо системы уравнений
(![]() )имеем
)имеем
![]() ;
(7)
;
(7)
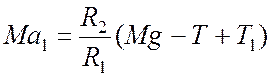 ;
(8)
;
(8)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.