Затухающие и вынужденные колебания. Величины их характеризующие. Вынужденные колебания. Резонанс

Тема 17 Затухающие и вынужденные колебания

1 Затухающие колебания. Величины их характеризующие.

2 Вынужденные колебания.

3 Резонанс.

Основные понятия по теме

При наличии в системе диссипативных сил амплитуда колебаний убывает с течением времени. Такие колебания принято называть затухающими колебаниями. Формально это означает, что в уравнение движения тела, совершающего свободные колебания, при описании затухающих колебаний, необходимо добавить слагаемые учитывающие диссипативные силы. В первом приближении величину этих сил принято считать пропорциональной скорости движения тела. В этом случае уравнение движения пружинного маятника (16.1) принимает вид

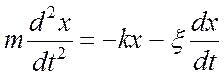,                                   (17.1)

   где коэффициент сопротивления.

Разделив обе части уравнения (17.1) на , перепишем его в виде

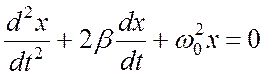.                                 (17.2)

В выражении (17.2) введены общепринятые обозначения 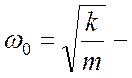собственная частота колебаний и 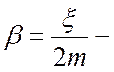коэффициент затухания.

Решение уравнения (17.2) имеет вид

.                            (17.3)

Здесь 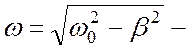частота затухающих колебаний, их начальная фаза. Функция  описывает убывание амплитуды затухающих колебаний с течением времени. График зависимости смещения  частицы из положения равновесия приведен на рисунке 17.1. Из вида приведенного графика следует принципиальный вывод – затухающие колебания являются негармоническими. Следовательно, величины используемые ранее для описания свободных колебаний, при описании затухающих колебаний непригодны. Исключение составляет только начальная фаза колебаний , так как она определяет начальные условия возбуждения колебаний и не связана с их дальнейшим поведением во времени.

Затухающие колебания принято характеризовать следующими величинами:

время релаксации колебаний. Время релаксации затухающих колебаний – это время, в течении которого их амплитуда уменьшается в  раз;

коэффициент затухания, который характеризует диссипативные силы в системе. Коэффициент затухания связан с временем релаксации очевидным соотношением

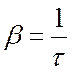                                                (17.4)

и, следовательно, имеет размерность ;

декремент затухания. Декремент затухания показывает, во сколько раз амплитуда затухающих колебаний убывает за время одного полного колебания, то есть

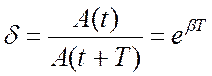;                                (17.5)

логарифмический декремент затухания;             (17.6)

добротность колебательной системы, характеризующая ее энергетические потери за время одного полного колебания. Добротность

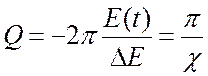,                                 (17.7)

где энергия, запасенная в системе в момент времени , потери энергии за время одного полного колебания.

Введенные выше понятия полностью характеризуют затухающие колебания, то есть описывают поведение кривых представленных на рисунке 17.1 в зависимости от времени. Обратное утверждение также является верным. Имея график зависимости , полученный экспериментально, можно определить все вышеназванные величины характеризующие затухающие колебания.

В реальных ситуациях затухание колебаний является неизбежным, но вредным явлением. Устранить его проявления в рассматриваемой колебательной системе можно, если в число сил, под действием которых происходят колебания, дополнительно включить вынуждающие силы, приводящие к компенсации потерь энергии в колебательной системе. Из основного условия, содержащегося в определении колебаний, «повторяемость во времени» следует, что вынуждающая сила должна иметь периодический характер

.                                       (17.8)

В выражении (17.8) амплитуда вынуждающей силы, ее частота.

При добавлении вынуждающей силы в уравнение движения (17.1), последнее, приобретая внешний вид

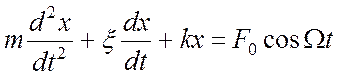,                           (17.9)

одновременно приобретает и качественно новое математическое свойство. В отличие от уравнений (16.1) и (17.1) уравнение (17.9) является неоднородным дифференциальным уравнением. Установившиеся вынужденные колебания описывает только частное решение неоднородного дифференциального уравнения (17.9), которое имеет вид

.                             (17.10)

Из (17.10) следует, что вынужденные колебания, так же как и свободные, являются гармоническими. Однако они отличаются от свободных колебаний рядом особенностей. Во первых, как ясно из выражения (17.10), частота  вынужденных колебаний равна частоте вынуждающей силы, то есть вынуждающая сила навязывает колебательной системе свою частоту. Во вторых, амплитуда вынужденных колебаний