Динамика материальной точки. Прямая и обратная задачи динамики. Законы Ньютона. Принцип независимости действия сил. Силы в механике

ТЕМА 4 ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ

1 Прямая и обратная задачи динамики.

2 Законы Ньютона.

3 Принцип независимости действия сил.

4 Силы в механике.

Вопросы для самоподготовки

1 Сформулируйте основную задачу динамики.

2 Сформулируйте первый закон Ньютона. В чем его сущность?

3 Какие системы отсчета называется инерциальными?, неинерциальными?

4 Может ли система отсчета, связанная с вращающимся телом, быть инерциальной?

5 Сформулируйте второй закон Ньютона. Запишите его в различных формах. Объясните разницу между ними.

6 Какой смысл имеет понятие силы в ньютоновской механике?

7 Назовите виды сил, рассматриваемых в механике.

8 Объясните механизм образования силы трения покоя. Чему равна величина  этой силы?

9 От каких факторов зависит сила трения скольжения? По какой формуле можно рассчитать эту силу?

10 Сформулируйте закон Гука. С каким явлением он связан?

11Что понимают под силами реакции? Сформулируйте правила определяющие их направления.

12 Опишите последовательность действий при решении основной задачи динамики.

Основные понятия по теме

Основная задача динамики состоит в определении законов движения материальной точки (1.1) или (1.4) по известным силам, действующим на эту точку со стороны других тел. Основную задачу динамики принято называть обратная задача динамики. Кроме того, в динамике рассматривается прямая задача – определение силы, действующей на точку, по известному закону ее движения. Решение как прямой, так и обратной (основной) задач динамики основано на использовании трех законов Ньютона.

Первый закон Ньютона постулирует существование инерциальных систем отсчета, то есть таких систем отсчета, в которых причиной изменения механического движения является только взаимодействие тел.

Существуют такие системы отсчета, в которых материальная точка (тело) сохраняет состояние покоя или равномерного прямолинейного движения до тех пор, пока взаимодействие с другими телами не заставит изменить ее это состояние. Мерой взаимодействия является сила.

Второй закон Ньютона (основной закон динамики) отвечает на вопрос, как изменяется механическое движение материальной точки под действием приложенной к ней силы. Сила, действующая на материальную точку, сообщает ей ускорение, которое в инерциальной системе отсчета пропорционально величине силы и имеет направление силы.

В аналитической форме этот закон записывается в виде основного уравнения динамики

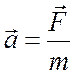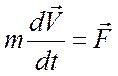    или    ,                                   (4.1)

где сила, действующая на материальную точку, масса материальной точки, являющаяся мерой ее инертных свойств.

Третий закон Ньютона отражает парный характер проявления сил. Силы, с которыми действуют друг на друга материальные точки, всегда равны по величине, противоположно направлены и действуют вдоль прямой соединяющей эти точки. Эти силы приложены к разным материальным точкам (телам), всегда действуют парами и являются силами одной природы.

Наряду с законами Ньютона фундаментальное значение для всей динамики имеет принцип независимости действия сил: если на материальную точку действует несколько сил, то ускорение точки равно векторной сумме ускорений, которые приобретает точка под действием каждой из этих сил в отдельности.

Принцип независимости действия сил позволяет заменить силы, действующие на точку, их равнодействующей

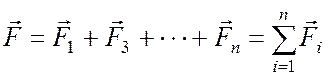                                  (4.2)

Согласно этому принципу силы и ускорения можно разлагать на составляющие, что существенно упрощает решение задач.

Силы, с которыми приходится иметь дело в механике, обусловлены двумя видами взаимодействия: гравитационным и электромагнитным. К гравитационным силам относятся:

сила тяжести – сила, с которой тело притягивается Землей

,                                                       (4.3)

где  масса тела,  ускорение свободного падения;

вес тела – сила, с которой тело действует на опору или растягивает подвес вследствие притяжения к Земле.

Примерами сил электромагнитной природы могут служить:

силы упругости – силы, возникающие в результате взаимодействия тел приводящего к их деформации. Например, сила упругости пружины при деформациях растяжения или сжатия

,                                                    (4.4)

где  жесткость пружины, ее абсолютная деформация;

силы трения – диссипативные силы сопротивления, действующие на тело и направленные противоположно относительного перемещения этого тела. Например, сила трения скольжения, возникающая при скольжении данного тела по поверхности другого,

,                                                  (4.5)

где коэффициент трения скольжения, сила нормального давления, прижимающая трущиеся поверхности друг к другу.

силы реакции – силы, действующие на данное тело со стороны связей, то есть тел, ограничивающих движение данного тела.

Примеры решения задач

1 Частица массой mдвижется в плоскости XY так, что  и , где А, В и положительные постоянные. Найти модуль и направление силы действующей на частицу.

Решение. В данном случае закон движения частицы задан в координатной форме. Следовательно, проекции ускорения частицы равны

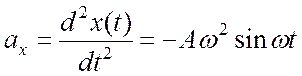 и .

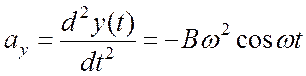Ускорение частицы, с учетом законов движения,

,

где радиус-вектор частицы.

Тогда, согласно второму закону Ньютона, сила, действующая на частицу,

.                                 (1)

Из (1) ясно, что сила  всегда направлена против радиус-вектора частицы.

Модуль силы

.

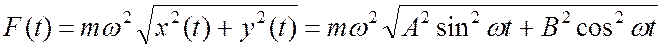В частном случае, при  (движение по окружности), модуль силы  не зависит от времени.

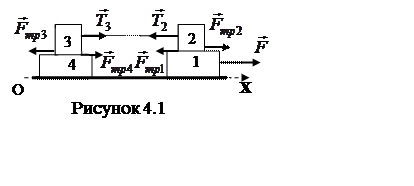
2 На гладком горизонтальном столе расположена система грузов 1, 2, 3 и 4, изображенная на рисунке 4.1. Массы грузов 2 и 3 одинаковы и равны m. Массы грузов 1 и 4 также одинаковы и равны М. Коэффициент трения между грузами m и M равен . Правый нижний груз тянут вдоль стола с силой , как показано на рисунке 4.1. Найдите ускорения всех грузов системы.