Проверка гипотез о параметрах нормально распределенной генеральной совокупности (Лабораторная работа № 2)

Лабораторная работа 2.

ПРОВЕРКА ГИПОТЕЗ О ПАРАМЕТРАХ НОРМАЛЬНО РАСПРЕДЕЛЕННОЙ ГЕНЕРАЛЬНОЙ СОВОКУПНОСТИ

1. Краткие теоретические положения

1.1. Основные понятия.

 Гипотеза – всякое утверждение, высказанное относительно неизвестного закона распределения генеральной совокупности или числовых характеристик этого закона распределения.

 Гипотеза, содержащая только одно утверждение – простая, иначе – сложная.

 Выдвинутая гипотеза называется нулевой . Альтернативная гипотеза  - гипотеза, противоположная .

Т. к. гипотезы проверяются с помощью статистических методов, то гипотезы – статистические.

Статистическая гипотеза – это закон распределения некоторой случайной величины. В реальной жизни эти гипотезы могут быть такими:

-  гипотезы об эффективности определенных лекарств;

-  гипотезы о росте доходов населения;

-  гипотезы об определении затрат или расходов и т. д.

Основными типами гипотез, которые проверяются статистическими методами, являются следующие:

1.  Гипотезы о типе закона распределения случайной величины.

Пусть   - выборка значений случайной величины . На основе выборки можно предположить, что функция распределения случайной величины  имеет конкретное распределение. Нужно проверить, не противоречит ли наше предположение опытным данным.

2.  Гипотезы об однородности двух или нескольких генеральных совокупностей или числовых характеристик.

 Например, по выборкам значений двух случайных величин  и  можно выдвинуть гипотезу об одинаковых законах распределения этих выборок или об одинаковых значениях средних, дисперсий.

 Например, можно проверить одинаковую эффективность двух видов лекарств или одинаковое качество товаров двух разных производителей.

3.  Гипотезы о числовых значениях параметров исследуемой генеральной совокупности.                                                                           

 Например, предположим, что математическое ожидание определенной случайной величины равно конкретному числу .

 Например, можно выдвинуть гипотезу о том, что вероятность сдачи экзамена определенным студентом равна 3/4.

1.2. Общая схема статистического критерия.

Правило проверки гипотез называется статистическим критерием.

Все критерии строятся по следующей схеме:

1.  Выдвигается нулевая гипотеза  и альтернативная ей гипотеза .

2.  Заранее выбирается уровень значимости . Т. к. гипотеза проверяется на основании конкретного числа опытных данных, то решение сопровождается определенной вероятностью ошибочного заключения, т. е. с вероятностью  гипотеза  может быть отвергнута, хотя на самом дел она справедлива, или, наоборот, с вероятностью  гипотеза может быть принята, хотя на самом деле она неверна. Вероятности ошибок должны быть маленькими и выбираются заранее.

Вероятность  ошибочного отклонения гипотезы  называется уровнем значимости статистического критерия.

К стандартным значениям  относятся  и другие.

Например,  означает, что в 5-ти случаях из 100 мы будем отвергать правильную гипотезу, но 5 ошибок из 100 случаев - это немного.

3.  Строится некоторая функция  от результатов наблюдений        , которая называется статистикой. Статистика  сама является случайной величиной и при определенной гипотезе  имеет определенный закон распределения.

4.  Из таблиц распределения статистики  находят критические значения для гипотезы  , т. е. два числа  и , которые всю числовую ось делят на 3 части:

1 часть называется областью недопустимо малых значений .

3 часть – область недопустимо больших значений .

Интервал   называется областью правдоподобных значений .

Требуется, чтобы вероятности недопустимо малых и больших значений были маленькими. Обычно их берут равными  , т. е.

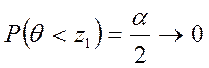  и  .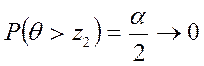

Тогда получаем:

,

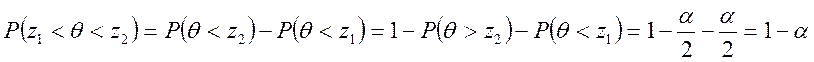т. к. , то .

 Число  называется доверительной вероятностью статистического критерия.

5.  В функцию  подставляют конкретные выборочные данные и находят конкретное число .

6.  Сравнивают вычисленное значение  с критическими значениями  и . Если  принадлежит области правдоподобных значений , то гипотеза  принимается с доверительной вероятностью . В противном случае гипотеза отвергается, и принимается альтернативная ей гипотеза.

При проверке гипотез можно допустить следующие ошибки:

1.  Ошибки первого рода – буде отвергнута правильная гипотеза , вероятность этой ошибки – уровень значимости .

2.  Ошибки второго рода – будет принята неверная гипотеза, вероятность ошибки находится более сложно.