Проверка гипотез о параметрах нормально распределенной генеральной совокупности (Лабораторная работа № 2), страница 3

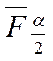Для выбранного уровня значимости  найдем такое число , для которого 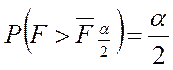, и число 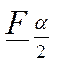, для которого 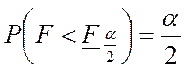. Отсюда легко получить следующее равенство:

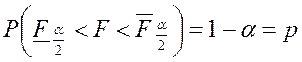, т. е. интервал  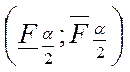является областью принятия гипотезы.

Затем по выборочным данным вычисляем значение .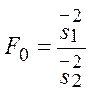

Если  принадлежит области принятия гипотезы, то гипотеза  принимается, в противном случае  отклоняется.

Замечание: число 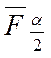 находится непосредственно по таблице.

Число .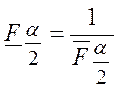

Пример. Давление в камере контролируется двумя манометрами. Для сравнения точности этих приборов фиксируются их показания. По результатам 10 замеров выборочные оценки оказались следующими:

 

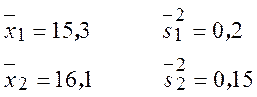
Проверить гипотезу о равенстве дисперсий при уровне значимости .

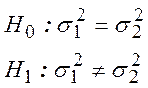
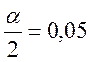
Число степеней свободы .

Находим по таблице  распределения число 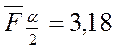, , 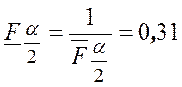т. е. .

По выборочным данным вычисляем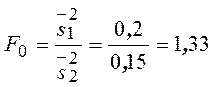  

, поэтому гипотеза о равенстве дисперсий принимается с вероятностью 0,9.

1.6. Проверка гипотез о законе распределения.

Проверка гипотезы о законе распределения критерием .

Допустим, что закон распределения случайной величины неизвестен. Однако по реальным значениям , полученным в результате опыта, эксперимента можно выдвинуть гипотезу о типе закона распределения . Нужно по выборке значений  проверить эту гипотезу.

 - неизвестный закон распределения СВ .

 - известный закон распределения СВ .

 Алгоритм проверки гипотезы о законе распределения критерием  состоит из следующих шагов:

1.  Все выборочные значения разбиваются на интервалов

2.  На основе предлагаемой гипотезы вычисляются вероятности попадания значений случайной величины в каждый из этих интервалов по формуле:  

 ,

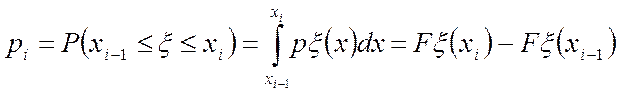   В результате получится значений .

3.  По данной выборке вычисляем наблюдаемое значение критерия:

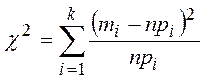 , где

 - число выборочных значений,

 - число выборочных значений, принадлежащих -тому интервалу, причем ,

 - вычисленное значение из пункта 2.

Если выдвинутая гипотеза о законе распределения верна, то  имеет распределение  с  степенями свободы.

4.  По заранее выбранному уровню значимости  по таблице распределения  находим такое число , для которого

  Тогда

 - это критическое значение для данной гипотезы. Если вычисленное значение  меньше табличного значения , то гипотеза  принимается с вероятностью . В противном случае гипотеза отвергается.

Пример. 70 человек приняло предложение испытать на себе новую диету. Эксперимент продолжался в течение 50 дней. При появлении побочных эффектов испытуемые отстранялись от участия.

 В результате были получены следующие данные:

Интервал (дни)	0-5	5-10	10-15	15-20	20-25	25-30	30-35	35-40	40-45	45-50
	2	12	8	4	14	6	10	2	1	11

 Является ли это распределение равномерным?

Составим статистический ряд:

	2,5	7,5	12,5	17,5	22,5	27,5	32,5	37,5	42,5	47,5
	2	12	8	4	14	6	10	2	1	11

: случайная величина имеет равномерное распределение, т. е.

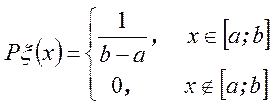
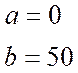
Тогда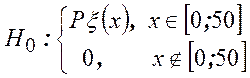

Известно, что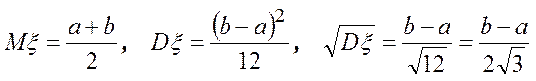

Вычислим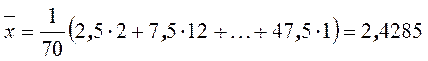

Считаем :

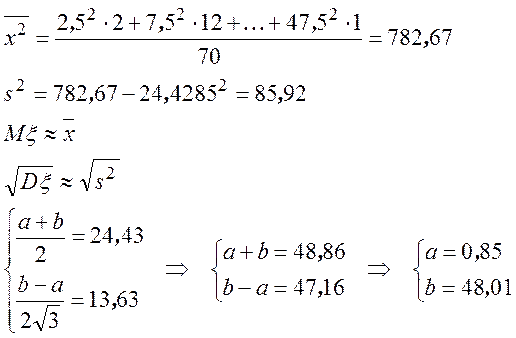
 Уточним формулировку гипотезы:

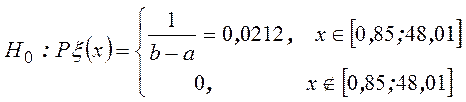
Вычислим вероятность  попадания в -тый интервал:

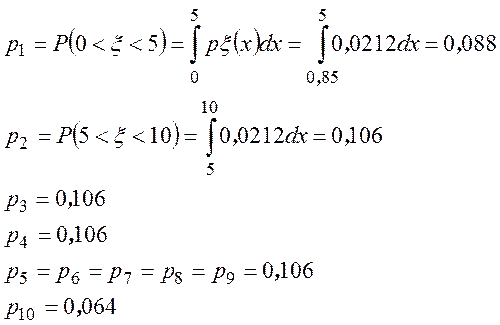
Вычислим по выборочным значениям выражение:

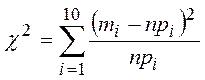
Для вычисления этого выражения составим таблицу:

1	0,088	6,16	2	-4,16	17,306	2,809
2	0,106	7,42	12	4,58	20,976	2,827
3	0,106	7,42	8	0,58	0,336	0,045
4	0,106	7,42	4	-3,42	11,696	1,276
5	0,106	7,42	14	6,58	43,296	5,835
6	0,106	7,42	6	-1,42	2,016	0,272
7	0,106	7,42	10	2,58	6,656	0,897
8	0,106	7,42	2	-5,42	29,376	3,959
9	0,106	7,42	1	-6,42	41,216	5,555
10	0,064	4,48	11	6,52	42,510	9,489