Проверка гипотез о параметрах нормально распределенной генеральной совокупности (Лабораторная работа № 2), страница 4

                                                                                                       

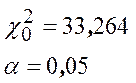
Число степеней свободы:

По таблице распределения  находим:

Т. к. , то гипотеза  о равномерном распределении отвергается, т. е. закон распределения числа испытуемых, на которых диета оказала побочные явления, не является равномерным.

            2. Задание.

По двум независимым выборкам из нормально распределенных генеральных совокупностей необходимо:

            1) при заданном уровне значимости  проверить нулевую гипотезу  о несовпадении (при  равенстве) математических ожиданий двух нормальных генеральных совокупностей, дисперсии которых неизвестны и равны ;

            2) при заданном уровне значимости  проверить нулевую гипотезу  о несовпадении (при  равенстве) математических ожиданий двух нормальных генеральных совокупностей, дисперсии которых неизвестны и различны ;

            3) при заданном уровне значимости ,  проверить нулевую гипотезу  о равенстве дисперсий двух нормальных генеральных совокупностей, математические ожидания которых неизвестны;

            4) проверить гипотезу о равномерном законе распределения.

1. Проверка нулевой гипотезы  в предположении, что  и неизвестны.

Альтернативные гипотезы: 1) ;

2) ;

3) .

Двухвыборочный t-тест с одинаковыми дисперсиями

	Переменная 1	Переменная 2
Среднее
Дисперсия
Наблюдения
Объединенная дисперсия
Гипотетическая разность средних	Число, равное предполагаемой разности средних .
df	Число степеней свободы  .
t-статистика	Наблюдаемое значение t-критерия .
P(T<=t) одностороннее	Если  (), то  ().
t критическое одностороннее	Критическое значение t-критерия определяется по таблицам распределения Стьюдента .
P(T<=t) двухстороннее	Если , то .
t критическое двухстороннее	Критическое значение t-критерия определяется по таблицам распределения Стьюдента .

Гипотеза  принимается, если.

Областью принятия гипотезы  для односторонних критериев является .

Областью принятия гипотезы  для двустороннего критерия является .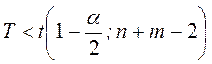

2. Проверка нулевой гипотезы  в предположении, что  и неизвестны.

Альтернативная гипотеза.

Двухвыборочный t-тест с различными дисперсиями

	Переменная 1	Переменная 2
Среднее
Дисперсия
Наблюдения
Гипотетическая разность средних	Число, равное предполагаемой разности средних .
df	Число степеней свободы , округленное до целого числа. В случае равных объемов выборок ()
t-статистика	Наблюдаемое значение t-критерия .
P(T<=t) одностороннее	Если  (), то  ().
t критическое одностороннее	Критическое значение t-критерия определяется по таблицам распределения Стьюдента .
P(T<=t) двухстороннее	Если , то .
t критическое двухстороннее	Критическое значение t-критерия определяется по таблицам распределения Стьюдента .

Гипотеза  принимается, если.

Областью принятия гипотезы  для односторонних критериев является интервал .

Областью принятия гипотезы  для двустороннего критерия является интервал .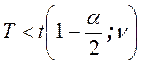

            3. Проверка нулевая гипотеза  в предположении, что математические ожидания  и  неизвестны.

Альтернативная гипотеза  ().

Двухвыборочный F-тест для дисперсии

	Переменная 1	Переменная 2
Среднее
Дисперсия
Наблюдения
df	Число степеней свободы
F	Наблюдаемое значение F .
P(F<=f) одностороннее	Если  (), то .
F критическое одностороннее	Критическое значение F-критерия определяется по таблицам распределения Фишера .

Гипотеза  принимается, если.

Областью принятия гипотезы  для правого одностороннего критерия является интервал .