Пусть случайные величины ![]() и
и ![]() имеют нормальное распределение. Пусть
имеют нормальное распределение. Пусть ![]() - выборка значений случайной величины
- выборка значений случайной величины ![]() , а
, а ![]() -
выборка значений случайной величины
-
выборка значений случайной величины ![]() . Допустим, что
. Допустим, что ![]() и
и ![]() известны.
Нужно проверить гипотезу о равенстве
известны.
Нужно проверить гипотезу о равенстве ![]() .
.
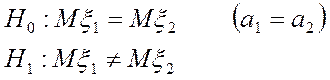
Выберем заранее уровень значимости ![]() .
.
Случайные величины ![]() и
и ![]() имеют нормальное распределение с параметрами
имеют нормальное распределение с параметрами
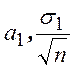 для
для ![]() и
и 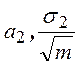 для
для ![]() .
.
Рассмотрим их разность ![]() ,
которая также имеет нормальное распределение. Найдем его параметры:
,
которая также имеет нормальное распределение. Найдем его параметры:
![]()
Заметим, что если гипотеза ![]() справедлива,
то
справедлива,
то ![]()
Найдем 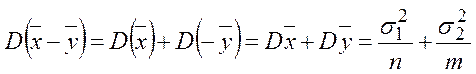
Рассмотрим случайную величину 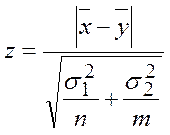
Очевидно, что случайная величина ![]() имеет стандартное нормальное распределение
(только при условии справедливости
имеет стандартное нормальное распределение
(только при условии справедливости ![]() ).
).
Найдем критические значения ![]() и
и
![]() , такие, что
, такие, что
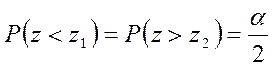
Тогда нетрудно получить ![]() .
.
Также нетрудно получить ![]()
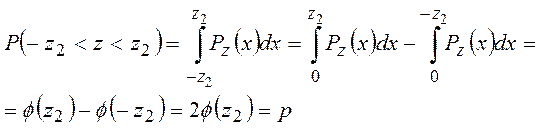
Отсюда  . По этому числу
находится значение
. По этому числу
находится значение ![]() .
.
В результате получится интервал ![]() для принятия гипотезы
для принятия гипотезы ![]() .
.
По выборочным данным находим значение 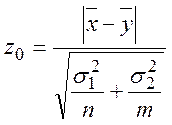
Если ![]() , то
, то ![]() принимается. В противном случае отвергается
в пользу принятия
принимается. В противном случае отвергается
в пользу принятия ![]() .
.
Пусть случайные величины ![]() и
и ![]() имеют нормальное распределение. Все их
параметры неизвестны, но дисперсии этих случайных величин равны. Нужно
проверить гипотезу о равенстве математических ожиданий по выборкам
имеют нормальное распределение. Все их
параметры неизвестны, но дисперсии этих случайных величин равны. Нужно
проверить гипотезу о равенстве математических ожиданий по выборкам ![]() значений случайной величины
значений случайной величины ![]() и
и ![]() значений
случайной величины
значений
случайной величины ![]()
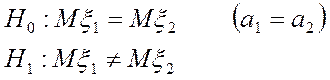
Выберем заранее уровень значимости ![]() . Построим случайную величину, имеющую
конкретное распределение.
. Построим случайную величину, имеющую
конкретное распределение.
В качестве оценки ![]() , в
качестве
, в
качестве ![]() .
.
В качестве оценки ![]() , а
, а ![]() .
.
![]()
Для
оценки ![]() используем обе выборочные дисперсии
используем обе выборочные дисперсии ![]() и
и ![]() .
.
Такая
оценка найдена и в качестве оценки ![]() выбирается
выбирается

Известно,
что ![]() имеет нормальное распределение с
параметрами
имеет нормальное распределение с
параметрами 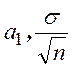 ,
, ![]() имеет
нормальное распределение с параметрами
имеет
нормальное распределение с параметрами 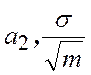 .
.
![]() имеет нормальное
распределение и
имеет нормальное
распределение и ![]() , а
, а
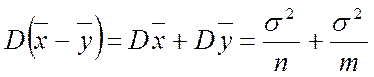
Если гипотеза ![]() верна,
то
верна,
то ![]()
Тогда случайная величина 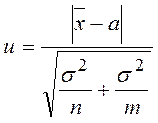 имеет
стандартное нормальное распределение.
имеет
стандартное нормальное распределение.
Случайные величины 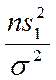 и
и 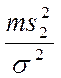 обе имеют распределение
обе имеют распределение ![]() соответственно с
соответственно с ![]() и
и
![]() степенями свободы.
степенями свободы.
Тогда их сумма 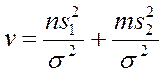 также
имеет распределение
также
имеет распределение ![]() с
с ![]() степенями
свободы.
степенями
свободы.
Вначале преобразуем выражение для ![]() :
:
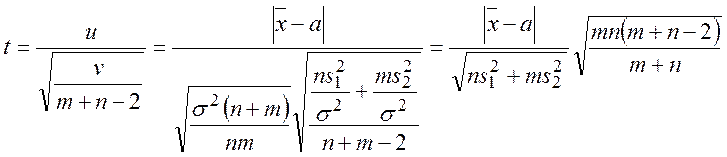
По таблице распределения Стьюдента для числа ![]() и числа степеней свободы
и числа степеней свободы ![]() находим число
находим число ![]() ,
такое, что
,
такое, что 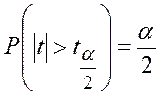 . Тогда интервал
. Тогда интервал 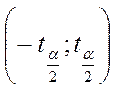 является
областью принятия гипотезы
является
областью принятия гипотезы ![]() . Затем по данным
выборкам вычисляем значение
. Затем по данным
выборкам вычисляем значение ![]() :
: 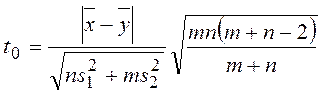
Если вычисленное значение  , то
гипотеза принимается с вероятностью
, то
гипотеза принимается с вероятностью ![]() . В обратном случае
гипотеза отвергается.
. В обратном случае
гипотеза отвергается.
Вероятность отклонения правильной гипотезы равна ![]() .
.
Пример. Используется 2 разных метода изготовления изделия. Чтобы проверить, одинаково ли материалоемки эти методы, собраны статистические данные о расходе сырья для каждого метода. Получили следующие данные:
|
1-й |
2 |
2,7 |
2,5 |
2,9 |
2,3 |
2,6 |
|
2-й |
2,5 |
3,2 |
3,5 |
3,8 |
3,5 |
- |
Предполагая, что среднеквадратические отклонения обоих методов равны, проверить гипотезу о том, что материалоемкость обоих методов одинакова.
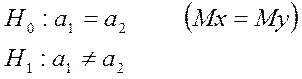
Выберем уровень значимости ![]() .
.
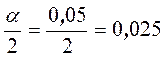
Подсчитаем число степеней свободы:
![]()
По таблице распределения Стьюдента для 9 и 0,025
находим 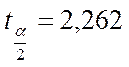
Это значит, что интервал ![]() является
областью принятия гипотезы
является
областью принятия гипотезы ![]() .
.
По выборочным данным найдем:
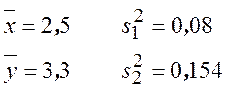
Считаем 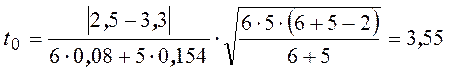
Очевидно, что![]() ,
поэтому
,
поэтому ![]() отклоняется. Принимается гипотеза
отклоняется. Принимается гипотеза ![]() . При этом можно сделать вывод о большей материалоемкости
второго метода.
. При этом можно сделать вывод о большей материалоемкости
второго метода.
Допустим, что случайные величины ![]() и
и ![]() обе
имеют нормальное распределение. Нужно по выборкам значений
обе
имеют нормальное распределение. Нужно по выборкам значений ![]() для случайной величины
для случайной величины ![]() и
и ![]() для
случайной величины
для
случайной величины ![]() проверить гипотезу о равенстве
дисперсий этих распределений.
проверить гипотезу о равенстве
дисперсий этих распределений.

Выберем заранее уровень значимости ![]() .
.
Найдем точечные оценки неизвестных дисперсий.
Пусть
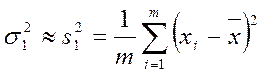 и
и 
По нашей гипотезе ![]() , т. е.
, т. е. ![]() и
и ![]() могут служить оценками для
могут служить оценками для ![]() . Известно, что случайные величины
. Известно, что случайные величины 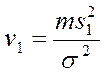 и
и 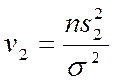 обе
имеют распределение
обе
имеют распределение ![]() соответственно с
соответственно с ![]() и
и ![]() степенями
свободы и являются независимыми случайными величинами.
степенями
свободы и являются независимыми случайными величинами.
Выберем наибольшее значение из ![]() и
и ![]() ,
например,
,
например, ![]() .
.
Рассмотрим случайную величину ![]() :
:
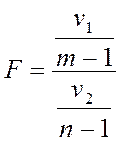 , которая имеет распределение Фишера с
, которая имеет распределение Фишера с ![]() степенями свободы.
степенями свободы.
Преобразуем выражение для ![]() :
:
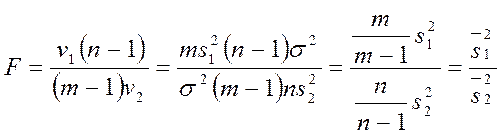 ,
,
т. е. 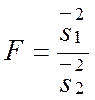 ,
поэтому можно было сразу находить несмещенные дисперсии по формуле:
,
поэтому можно было сразу находить несмещенные дисперсии по формуле:
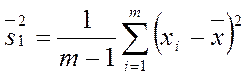 и
и 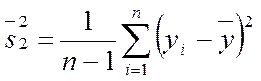 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.