1. Решение ОДУ. Формула Эйлера. Формула Рунге-Кута. Формула Адемса. Погрешность.
Задача Коши:
у'=f(x,y)
y(x0)= y0.
Методы решения ОДУ: 2 класса: одно и многошаговые методы.
Рассмотрим одношаговые методы.
Метод Эйлера:
Пусть неизвестна т. (xm,ym) искомой кривой. Проведем прямую линию с tg угла наклона у'm=f'(xm,ym) проходящею через точку (xm,ym). Уравнение этой прямой y=y m= у'm(x-xm)= f(xm,ym)(x-xm). Следующая точка приближения та, где прямая пересечет вертикаль проходящею через точку xm+1=xm+h.
![]()

 L
L
l у'(x)
 |
|||||
 |
|||||
уm уm+1
![]()
xm xm+1=xm+h
ym+1=ym+ уm'h
уm'= f(xm,ym). (1)
Решение по (1) согласуется с разложением в ряд Тейлора, вплоть до членов порядка h. Этот метод является методом Рунге-Кута 1-го порядка.
Погрешность. Ошибка ограничения e=kh2, k=const.
Исправленный метод Эйлера:
В этом методе находится средний tg угла наклона касательной для 2-х точек (xm,ym) и Î (средний tg угла наклона)=(xm+h, ym+ hy'm).
Î 

 L1 L2
L1 L2
![]()

 L
L
l у'(x)
 |
|||||
 |
|||||
уm уm+1
![]()
xm xm+1=xm+h
Алгоритм:
1. с помощью метода Эйлера находим точку(xm+h, ym+ hy'm), лежащую на L1, с tg угла наклона уm'= f(xm,ym).
2. в этой точке снова вычисляется tg угла наклона касательной f(xm+h, ym+ hy'm) и проводится прямая L1.
3. усреднение этих tg-ов дает Î, tg ее угла наклона= 1/2[f(xm,ym)+f(xm+h, ym+ hy'm)] (2)
4. через т. (xm,ym) проводим прямую // Î. Уравнение этой прямой: y- ym= Ф(xm,ym,h) (xm,ym).
Точка в которой L пересечет вертикаль, проходит через точку xm+1= xmh, и будет искомой (xm+1,ym+1).
ym+1= ym+hФ(xm,ym,h). (3).
Формула Рунге-Кута.
ym+1= ym+hФ(xm,ym,h), где Ф(xm,ym,h)=а1f (xm,ym)+ а2f (xm+b2h, ym+ b2hy'm).
y'm= f(xm,ym).
am,bm - const.
В частности, для исправленного метода Эйлера: am=1/2, bm=1.
2. Вариационное исчисление. Симплекс-метод - определение. Критерий оптимальности. Алгоритм.
Основной метод ЛП - СМ, разработанный для специальной задачи в канонической форме:
c'x→max, Ax=b, x≥0. (1)
ЦФ - maxимизируется, а все переменные имеют ограничения.
Введем обозначения:
J={1,…,n} - множество индексов переменной xj.
I= {1,…,m} - множество #-ов основных ограничений.
aj=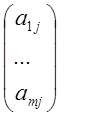 Є Rm
Є Rm
- j-ый столбец матрицы А. Вектор х Є Rm - базисный план (1), . если он удовлетворяет всем ограничениям задачи, и его переменные разбиты на 2 группы: 1. базисные: xj1,… xjm.; и 2. не базисные xj, j Є Jh=J\JБ. Причем: 1. xj=0, j Є Jh.; 2. aj, jЄJБ - линейно независимы в Rm. 3. Если составить матрицу АБ= (aj, jЄJБ), то det АБ≠0. Эта матрица называется базисной.
![]()
![]()
![]()
![]()
![]() Критерий оптимальности: Пусть известен БП (xj, JБ), тогда:
∆н≥0 - достаточно, а для невыражденного БП необходимо для его оптимальности.
Критерий оптимальности: Пусть известен БП (xj, JБ), тогда:
∆н≥0 - достаточно, а для невыражденного БП необходимо для его оптимальности.
Достаточно: пусть ∆н= хн
- хн ≥0., хн ≥0, хн =0.![]()
![]() Тогда: с'х - c'x, для всех
х ЄХ, х - оптимум.
Тогда: с'х - c'x, для всех
х ЄХ, х - оптимум.
Необходимо: Пусть х -ОБ и невырожденный план → хБ >0.
Предположим противное, т.е. существует j0ЄJн: ∆j0<0.
Построим вектор приращений ∆х с.о.: пусть ∆хj=0, j Є Jh\r0, а ∆хj0= Θ≥0.
Базисные компоненты приращений подбирают т.о. что бы оставалось А∆х=0 и ∆хБ= -А-1БАн∆хн.
При выполнении этих условий вектор ∆х будет удовлетворять основным ограничениям задачи (1). →
∆хБ= - ΘА-1БАнaj0. Построим вектор хн = х+∆х.
Θ можно подобрать т.о., ч.б. вектор х был планом задачи, т.е. х>0.
![]() Тогда, план
х лучше х, т.е. получаем противоречие с оптимальностью х.
Тогда, план
х лучше х, т.е. получаем противоречие с оптимальностью х.
Алгоритм:
Пусть имеется объект, поведение которого надо оптимизировать.
1. изучение и описательное регулирование.
а) изучение структуры объекта.
б) изучение основных способов функционирования составных частей.
в) выясняют цель оптимизации.
г) собирают конкретную цифровую информацию о структуре функции и цели объекта.
2. Математическое моделирование.
а) построение неизвестных параметров х1,…,хn, которые однозначно описывают поведение объекта изменением которых можно выполнить достижение цели.
б) запись основных связей и закономерностей функционирования объекта с помощью введенных неизвестных хj и мат. операций. В результате приходим к системе ограничений на хj. В совокупности все эти ограничения и задают множество планов Х, а именно: вектор х т.т.т. является планом, есди он удовлетворяет всем ограничениям одновременно.
в) запись с помощью неизвестных и мат. операций ЦФ f(x).
После чего, мы приходим к задаче в форме (1).
3. Теоретическое исследование и выбор метода, вкл. в себя:
а) выяснение к какому классу задач оптимизации относится наша.
б) изучении теории по данному классу задач и методах которые для него имеются. Если нет, то работают доп. исследования, учитывающие специфику задачи. Модифицируется или разрабатывается новый метод.
4. Построение ОП.
а) выясняем им-ся ли программа реализации нашего метода: Да- то используем; Нет- строим свою.
б) вводим в программу числовые параметры конкретной задачи.
5. Исследование. Сравнивается полученный ОП с реальным поведением объекта. Если есть возможность, то проводим эксперимент.
Если решение нас не удовлетворяет, то процесс решения задачи оптимизации может быть улучшен на всех этапах 1-4. При решении задачи оптимизации, возможны ошибки погрешности во всех 5 пунктах.
3. Принцип Лагранжа снятия ограничений для задач с ограниченными равенствами.
По параметрам задачи c'x→max, Ax=b, x≥0, вводим функцию Лагранжа.
![]()
![]()
![]()
![]()
![]() F(x,λ)= λf(x)+ Σλigi(x)=
λ0f(x)- x0λ(x) - обобщенная
функция Лагранжа.
F(x,λ)= λf(x)+ Σλigi(x)=
λ0f(x)- x0λ(x) - обобщенная
функция Лагранжа.
F(x,λ)= f(x)+ λ'g(x).
λ=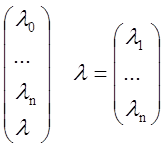 λi - множители Лагранжа.
λi - множители Лагранжа.
λ - обобщенный λ - классический вектор Лагранжа.
F(x,λ)λ0=1 = F(x,λ).
Обобщенное правило Лагранжа:
если Х0 - ЛОП, тогда существует такой обобщенный вектор Лагранжа λ0, λ0≠0. 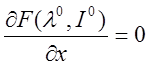 .
.
Из числа задач 1 можно выделить такой подкласс, который с одной стороны является достаточно широким, ему принадлежат практически все задачи возникающие в приложениях, а с другой стороны, для которых правило Лагранжа справедливо в классической форме (λ00=1).
Обобщенное и
классическое правило Лагранжа вместе образуют т.н. принцип Лагранжа снятия
ограничений, согласно которого ОП и ЛОП задачи (1) следует искать среди решений
системы 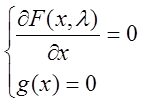 и системы
и системы 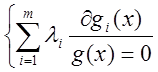 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.