Случайные величины. Закон распределения дискретной случайной величины. Функция распределения ДСВ. Непрерывные случайные величины. Квантили и процентили

ЛЕКЦИЯ 4

СЛУЧАЙНЫЕ ВЕЛИЧИНЫ.

4.1.Понятие случайных величин. 1

4.2. Закон распределения дискретной случайной величины. 1

4.3. Функция распределения ДСВ. 2

4.4. Свойства функции распределения: 2

4.5. Непрерывные случайные величины. 3

4.6. Плотность вероятности и ее свойства. 3

4.7. Квантили и процентили. 4

4.8.  Математическое ожидание. Мода. Медиана. 4

4.9. Дисперсия СВ и ее свойства. 6

4.1.Понятие случайных величин.

            Понятие случайной величины в теории вероятностей является фундаментальным. В разделе 1 рассматривался опыт со случайным исходом. Событие является качественной характеристикой опыта. Но случайный результат опыта можно охарактеризовать и количественно (число бракованных изделий среди отобранных, число попаданий в мишень при 6 выстрелах, время безотказной работы ЭВМ между двумя сбоями).

            Случайные величины обозначаются буквами греческого алфавита: x, h, m, а возможные значения случайной величины обозначаются маленькими латинскими буквами , ,.

            Различают 2 вида случайных величин: дискретные и непрерывные.

            О.4.1. Дискретной случайной величиной называется такая величина, число значений которой либо конечно, либо счетно.

            Пример. Дискретные (ДСВ):

x = {0,1,2,3,4,5}

x = {число попаданий в мишень при 3 выстрелах}

x = {0,1,2,3}

x = {число вызовов на телефонную станцию}

x = {1,2,…}

x = {число извлеченных деталей до первой бракованной}

x = {1,2,…}

            О.4.2. Непрерывной случайной величиной называется такая случайная величина, возможное значение которой непрерывно заполняет некоторый интервал числовой оси. Число возможных значений непрерывной случайной величины бесконечно.

            Пример. Непрерывные (НСВ):

x = {время непрерывной работы ЭВМ между сбоями}

x = [0;∞)

x = {диаметр изготовленной детали}

ξ  = [d - e £ x £ d + e]                      d – диаметр  e - отклонения.

            Случайная величина  считается изученной, если известны ее возможные значения и вероятности всех возможных значений.

4.2. Закон распределения дискретной случайной величины.

            Пусть задана ДСВ, возможные значения которой есть , , , . В результате опыта случайная величина принимает одно из своих возможных значений, т. е. произойдет одно событие из полной группы несовместных событий: , , , .

Обозначим вероятности этих событий

, , , .

Так как эти события образуют полную группу, то .

            О.4.3. Законом распределения дискретной случайной величины  называется множество всех пар , , , .

            Чаще всего закон распределения записывается в виде таблицы – ряд распределения.

                      Пример. В урне имеется 3 белых и 4 черных шара. Построить закон распределения числа вынутых белых шаров

Решение.

x = {число вынутых белых шаров в выборке}

.

4.3. Функция распределения ДСВ.

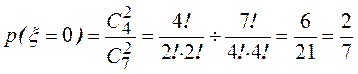
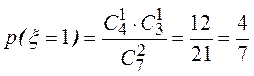
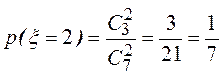            О.4.4. Законом распределения случайной величины x называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими вероятностями.

            Ряд распределения является законом распределения. Но для непрерывной случайной величины ряд распределения построить невозможно, т. к. она имеет бесконечное множество значений, которые заполняют некоторый промежуток.

            Наиболее общим законом распределения является функция распределения.

            О.4.5. Функцией распределения случайной величины x называется функция переменной , равная вероятности того, что случайная величина примет значение , где .

.

            Из определения следует, что функция распределения существует как для НСВ, так и для ДСВ. Она полностью характеризует СВ с вероятностной точки зрения. Следовательно, является законом распределения.

            Геометрический смысл функции распределения:

Если рассматривать СВ x как случайную точку оси ОХ, которая может принять то или иное значение в результате опыта, то функция распределения  есть вероятность того, что случайная точка x находится левее точки .

            Пример. В урне 3 белых и 4 черных шара. Извлекается 2 шара. Построить функцию распределения числа белых шаров в выборке.

Решение. x = {число белых шаров в выборке} 

,

,

,

.

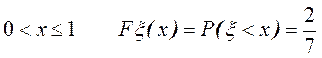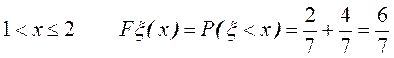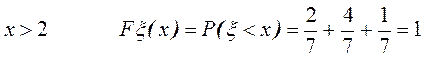Тогда

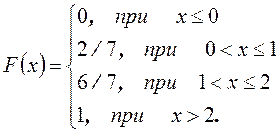
Графиком функции является ступенчатая ломаная линия.

Функция распределения находится как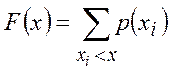

4.4. Свойства функции распределения:

            1.

Это свойство следует из того, что функция распределения есть вероятность.

            2. Функция распределения F (x) всегда неубывающая функция, т. е  имеем .

►Пусть события

,

.◄

           3.    

    

            4.

            5. (только для дискретных случайных величин)Функция распределения  всегда непрерывна слева

.

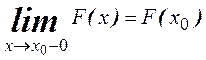            Если СВ x принимает возможное значение  с вероятностью , то ее функция распределения  имеет в точке  разрыв первого рода со скачком _i

.

4.5. Непрерывные случайные величины.

            Любая функция  непрерывна слева, но не любая – справа. Функция распределения дискретной случайной величины не является непрерывной справа. Особый интерес вызывают те функции, которые непрерывны во всех точках.

            Случайная величина x является непрерывной, если ее функция распределения непрерывна.

Функция распределения НСВ обладает первыми четырьмя свойствами предыдущего пункта.

            Теорема. Для любого действительного числа  вероятность того, что НСВ примет значение, равное , равна 0.

►

◄

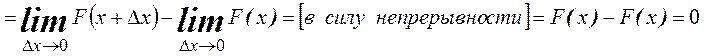            Данная теорема означает, что любое свое значение НСВ принимает крайне редко, т. к. у нее бесконечное множество значений.