Следствие: ![]() .
.
О.4.6. Плотностью вероятности
непрерывной случайной величины ![]() называется производная
ее функции распределения.
называется производная
ее функции распределения.
![]()
![]() .
.
Свойства ![]() :
:
1. ![]() .
.
►Т.к. ![]() – неубывающая функция, то
– неубывающая функция, то
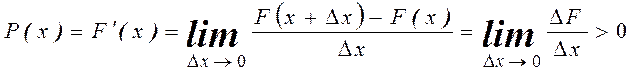 ◄
◄
Это свойство означает, что график функции ![]() лежит не ниже оси
лежит не ниже оси ![]() .
.
2. 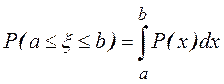
►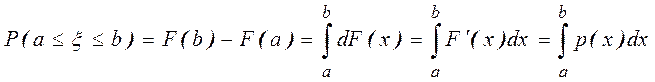 ◄
◄
3. Функция распределения выражается
через плотность вероятности как 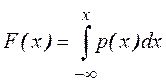 .
.
►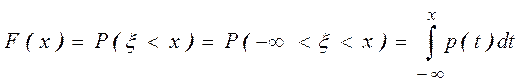 .◄
.◄
4. Условие нормировки 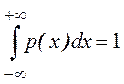 .
.
►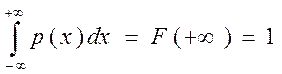 ◄
◄
Условие нормировки означает, что площадь
криволинейной трапеции, ограниченна сверху графиком функции ![]() , снизу осью
, снизу осью ![]() .
.
5. Вероятность конкретного значения ![]() .
.
►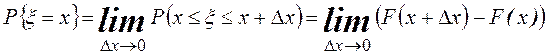
Отсюда
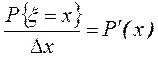 . Тогда
. Тогда ![]() .◄
.◄
Произведение ![]() есть
площадь прямоугольника со сторонами
есть
площадь прямоугольника со сторонами ![]() и
и ![]() . Чем больше значение площади, тем
больше плотность.
. Чем больше значение площади, тем
больше плотность.
Пусть СВ x имеет функцию распределения ![]() . Функция
. Функция
![]() ставит произвольному действительному числу
ставит произвольному действительному числу
![]() вероятность
вероятность ![]() , т. е.
, т. е. ![]() . Иногда приходится решать обратную задачу: по заданному значению
. Иногда приходится решать обратную задачу: по заданному значению ![]() найти такое действительное число
найти такое действительное число ![]() , для которого
, для которого ![]() .
.
О.4.7. Число ![]() называется
квантилью, если для него выполняется условие
называется
квантилью, если для него выполняется условие ![]() .
.
Из определения НСВ x следует, что ее функция
распределения так же непрерывна. Поэтому для НСВ число ![]() является
решением уравнения
является
решением уравнения ![]() .
.
Пример. Найти квантиль, соответствующую
вероятности 1/5 для функции 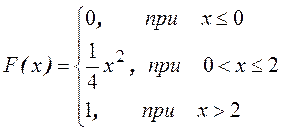 .
.
Решение.
Так как ![]() , то
, то 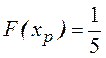 .
Подставляя, имеем
.
Подставляя, имеем 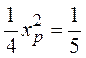 .
Отсюда
.
Отсюда 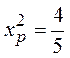 .
.
Так как
![]() , то
, то 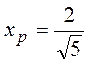 .
.
Квантиль, которая соответствует значению ![]() называется медианой:
называется медианой:
Например, 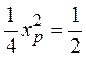 . Отсюда
. Отсюда ![]() . Тогда
. Тогда ![]() –
медиана.
–
медиана.
Если вероятность задана в процентах, то
квантиль ![]() называется процентилью или
процентной точкой.
называется процентилью или
процентной точкой.
Например, р% = 50%
В таблицах по математической статистике (Большов-Смирнов) заданы процентные точки и соответствующие им квантили. Наиболее часто используются квантили, которые соответствуют вероятности р = 0,01; 0,05; 0,1 (1%, 5%, 10%).
О.4.8.
Математическим ожиданием ДСВ x
называется число 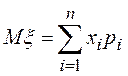 , где
, где ![]() –
возможные значения СВ,
–
возможные значения СВ, ![]() – соответствующие вероятности.
– соответствующие вероятности.
Если ряд сходится, математическое ожидание существует. В противном случае – нет.
Математическим ожиданиемНСВ называется число 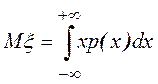 .
.
Если интеграл абсолютно сходится, то математическое ожидание существует. В противном случае – нет.
Пример. Пусть СВ x принимает значения ![]() и пусть
и пусть ![]() встречается
встречается ![]() раз, …,
раз, …, ![]() встречается
встречается ![]() раз.
Тогда
раз.
Тогда ![]() и среднее значение
и среднее значение
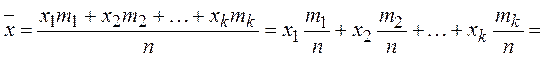
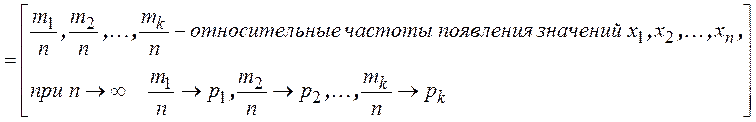
![]() .
.
Итак, ![]() для
ДСВ стремится к Мx, поэтому можно говорить о том, что Мx характеризует среднее значение СВ x.
для
ДСВ стремится к Мx, поэтому можно говорить о том, что Мx характеризует среднее значение СВ x.
Свойства математического ожидания Мx:
1. Если x = const = c, то Mc = C
2. Постоянный множитель можно выносить за знак
математического ожидания ![]() .
.
3. Математическое ожидание от суммы СВ равно сумме математических ожиданий
![]() .
.
4. Если СВ ![]() и
и ![]() независимы,
то
независимы,
то ![]()
5. Если
значения СВ попадают в интервал [a;b], то ![]()
6. Если СВ h = j(x), то
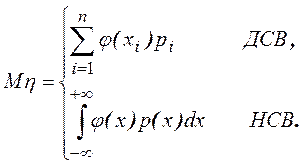
Примеры.
· Дискретная случайная величина x задана рядом распределения. Найти математическое ожидание.
Решение.
|
Мx |
-1 |
0 |
1 |
|
Р |
0,2 |
0,5 |
0,3 |
Мx = -1*0,2 + 0*0,5 + 1*0,3 = -0,2 + 0,3 = 0,1
·
Вычислить
математическое ожидание непрерывной случайной величины, заданной плотностью
вероятности 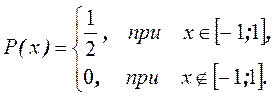
Решение.
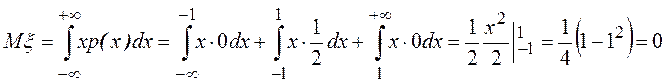 .
.
О.4.9. Модой (Моx) случайной величины x называется ее наиболее вероятностное значение.
В случае если x - ДСВ, то Моx - значение СВ с наибольшей вероятностью. Если x - НСВ, то Моx - точка максимума плотности вероятности Р(х).
О.4.10. Медианой
СВ x называется
такое ее значение ![]() , для которого вероятность того,
что
, для которого вероятность того,
что ![]() равна 0,5.
равна 0,5.
В случае ДСВ число![]() находится из системы уравнений
находится из системы уравнений 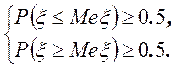
Пример. Найти моду и медиану СВ, заданной рядом распределения:
Моx = 0 Меx = 0
Р(x³0) = Р(x=0) + Р(x=1) = 0,5 + 0,3 = 0,8³0,5
Р(x£0) = Р(x=-1) + Р(x=0) = 0,2 + 0,5 = 0,7³0,5
Математическое ожидание, мода, медиана являются характеристиками положения СВ. При проведении конкретных исследований или измерений полученные результаты практически всегда отличаются от средней. Важно знать, насколько возможно отклонение практического результата от математического ожидания. Для этого вводится другая числовая характеристика, которая характеризует меру разброса значений СВ около математического ожидания.
О.4.11. Дисперсией
СВ x называется
число ![]() .
.
Дисперсия существует, если она равна конечному числу.
Если x - ДСВ, то дисперсия:
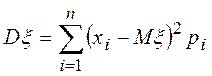
Если x - НСВ, то дисперсия:
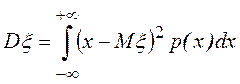
Свойства дисперсии:
1. Дисперсию можно вычислить по формуле
![]()
►По определению
![]()
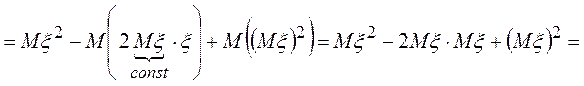
![]() .◄
.◄
2. Dx ³ 0
3. Если x = const = с, то Dc = 0
4. Если a - const, то дисперсия:![]()
5. Если x1, x2 – независимы, то дисперсия: ![]()
6. Если x1, x2 – зависимы, то дисперсия: равна
![]() ,
,
где ![]() .
.
7. Если x1, x2, …, xn попарно независимы, то дисперсия
![]() .
.
Дисперсия может быть вычислена по формулам
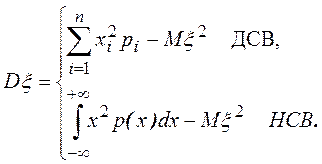
Чем меньше дисперсия, тем больше вероятность попадания значений СВ в малый интервал около математического ожидания.
Пример. СВ x задана рядом распределения
|
x |
-2 |
-1 |
0 |
1 |
2 |
|
p |
0,1 |
0,3 |
0,2 |
0,3 |
0,1 |
Найти дисперсию СВ.
Решение.
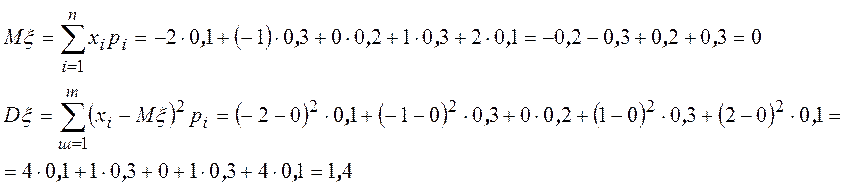
О.4.12. Средним
квадратичным отклонением s называется число![]() .
.
Пример. ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.