п. 1.2. События и операции над ними.
Относительные частоты и их свойства
Первичным понятием теории вероятностей, неопределяемым через другие понятия, является пространство элементарных исходов Ω. Обычно в качестве пространства элементарных исходов берутся единственно возможные неразложимые результаты эксперимента.
Пример
1.
Предположим, что бросается
симметричная монета. Тогда ![]() (герб и решка).
(герб и решка).
2.
Игральная кость ![]() .
.
3.
Бросаются две монеты ![]() .
.
4.
Бросаются две игральных кости ![]() . Число элементарных исходов 36.
. Число элементарных исходов 36.
5.
На [AB] числовой оси
w бросается наудачу точка. ![]()
6.
На [AB] бросаются
две точки ![]() .
.
B
 y
y
x
Определение. Событием называется произвольное подмножество А пространства элементарных исходов Ω. Те элементарные исходы, из которых состоит событие А, называются благоприятствующими событию А.
Говорят,
что событие А произошло, если в результате эксперимента происходит
элементарный исход w![]() A,
т.е. благоприятствующий событию А.
A,
т.е. благоприятствующий событию А.
Рассмотрим
пример 2. ![]() ,
, ![]() –событие,
состоящее в выпадении нечетного числа очков;
–событие,
состоящее в выпадении нечетного числа очков; ![]() –событие,
состоящее в выпадении четного числа очков.
–событие,
состоящее в выпадении четного числа очков.
o Все пространство элементарных исходов Ω, если взять в качестве события, называют достоверным событием, поскольку оно происходит в любом эксперименте (всегда).
o
Пустое множество ![]() (т.е. множество, которое не содержит ни
одного элементарного исхода) называется невозможным событием, поскольку
оно никогда не происходит.
(т.е. множество, которое не содержит ни
одного элементарного исхода) называется невозможным событием, поскольку
оно никогда не происходит.
Все остальные события, кроме Ω и ![]() , называются случайными.
, называются случайными.
Операции над событиями.
0.1
Суммой событий А и В называется объединение этих множеств А![]() B.
B.
![]() или
или ![]() .
.
![]() –событие, которое
происходит тогда и только тогда, когда происходит хотя бы одно из событий А или
В.
–событие, которое
происходит тогда и только тогда, когда происходит хотя бы одно из событий А или
В.
0.2
Произведением событий А и В называется пересечение множеств А и В,
т.е. А![]() В. Обозначается как АВ.
В. Обозначается как АВ.
АВ–событие, когда А и В происходят одновременно.
![]() и
и ![]() .
.
0.3 Разностью событий А и В называется разность множеств А\В.
А\В–событие, которое происходит <=>, когда происходит А и не происходит В.
![]() и
и ![]() .
.
o
События А и В называются несовместимыми,
если ![]() . Если А и В несовместимы, то будем
обозначать
. Если А и В несовместимы, то будем
обозначать ![]() .
.
o
Говорят, что событие А влечет
событие В, если А является подмножеством В, т.е. ![]() (когда
происходит А, происходит В).
(когда
происходит А, происходит В).
![]() .
.
o
Событие 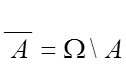 называется
противоположным к событию А.
называется
противоположным к событию А.
Пример 2. 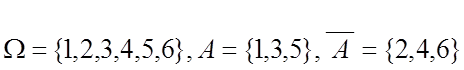 .
. ![]() происходит тогда, когда А не происходит.
происходит тогда, когда А не происходит.
o
Говорят, что события Н1,Н2,…,Нn образуют
полную группу, если Н1+Н2+…+Нn=Ω
(т.е. Н1, Н2, Нn–несовместимы,
т.е. Нi Нj=![]() ,
если i≠j).
,
если i≠j).
Например, А и ![]() образуют
полную группу:
образуют
полную группу: 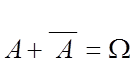 .
.
Предположим, что производится некоторый случайный
эксперимент, результат которого описывается пространством Ω. Произведем N
экспериментов. Пусть А—некоторое событие (![]() ), N(A)—число
тех экспериментов, в которых произошло событие А.
), N(A)—число
тех экспериментов, в которых произошло событие А.
Тогда число 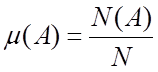 называется
относительной частотой события А.
называется
относительной частотой события А.
Свойства относительных частот.
Свойство 1.
Относительная частота
произвольного события А. ![]()
![]() .
.
Свойство 2.
Относительная частота
достоверного события равна 1. 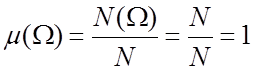 .
.
Свойство 3.
(Аддитивность) Относительная частота суммы несовместимых событий 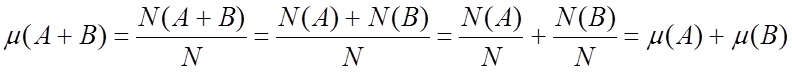
§2. Аксиомы теории вероятностей.
Пусть Ω—пространство элементарных исходов. Предположим, что F—некоторый класс подмножеств Ω.
o
Событие—это подмножество Ω,
принадлежащее классу F. Любому ![]() ставится в соответствие
действительное число P(A), называемое вероятностью А, так что
при этом выполняется аксиомы:
ставится в соответствие
действительное число P(A), называемое вероятностью А, так что
при этом выполняется аксиомы:
Аксиома 1.
![]()
![]()
Аксиома 2.
![]() ,т.е. вероятность достоверного события равна
1.
,т.е. вероятность достоверного события равна
1.
Аксиома 3.
(счетной аддитивности) Если ![]() и
и ![]() , то
, то 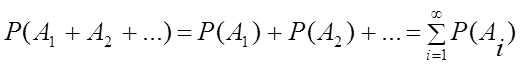 (для несовместимых событий).
(для несовместимых событий).
§ 3 Дискретные пространства элементарных исходов.
Классическое определение вероятности.
o Бесконечное множество называется счетным, если элементы этого множества можно занумеровать числами натурального ряда (натуральными числами).
Все другие бесконечные множества называются несчетными. Примером несчетного множества может служить [а,b], счетного N.
o
Пространство элементарных исходов
называется дискретным, если оно конечно или счетно, т.е. ![]() или
или ![]() .
.
Любому элементарному исходу 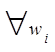 ставится в соответствие число
ставится в соответствие число ![]() , так что при этом
, так что при этом 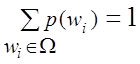 .
Т.е.
.
Т.е. ![]()
o
Вероятностью события А называется
число 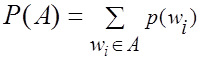 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.