Пример.
Бросаем игральную кость ![]() —дискретное
пространство элементарных исходов.
—дискретное
пространство элементарных исходов. ![]() . Р (выпадает нечетное
количество очков)=
. Р (выпадает нечетное
количество очков)=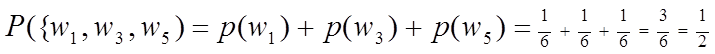
Сделаем следующие предположения:
1.
Пространство элементарных исходов ![]() —конечно.
—конечно.
2.
Все элементарные исходы
равновозможны (равновероятны), т.е. ![]() . Тогда получим
. Тогда получим ![]() , т.к. слагаемые равны, то имеем
, т.к. слагаемые равны, то имеем ![]() , т.е.
, т.е. 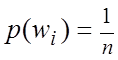 , где
, где ![]() . Рассмотрим некоторые события
. Рассмотрим некоторые события 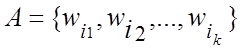 , где k≤n.
Вероятность события А.
, где k≤n.
Вероятность события А.![]()
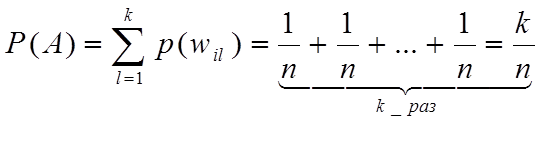
o
Если пространство элементарных
исходов конечно, а все элементарные исходы равновероятны, то вероятностью
события А называется отношение числа элементарных исходов, благоприятствующих
событию А к общему числу элементарных исходов: 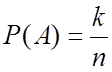 .
.
Это классическое определение вероятности.
Примеры:
1. Бросается игральная кость. Какова вероятность выпадения нечетного числа очков?
![]() , n=6;
, n=6; ![]() , k=3;
, k=3; 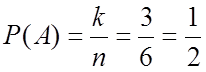 .
.
2. Бросаются две монеты. Какова вероятность того, что хотя бы на одной выпадет герб?
![]() ,
, ![]() ,
, 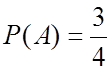 .
.
3. Бросаются две игральные кости. Какова вероятность того, что сумма выпавших очков равна семи?
![]() , n=36;
, n=36;
![]() , k=6;
, k=6;
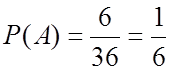 .
.
§4. Элементы комбинаторики.
Лемма 1. Из m элементов а1,…,аm первой группы и n элементов b1,…,bn второй группы можно составить ровно m∙n упорядоченных пар вида (аi, bj), содержащих по одному элементу из каждой группы.
Доказательство:
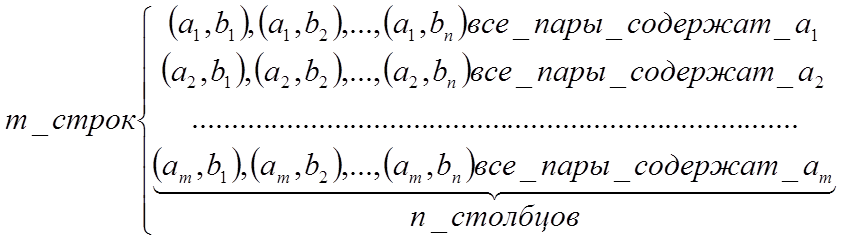
Всего имеем m∙n пар.
Пример. В колоде 4 масти (черва, пика, трефа, бубна), в каждой масти по 9 карт. Итого n=4∙9=36.
Лемма 2. Из n1 элементов первой группы a1, а2,…, аn1,
n2 элементов второй группы b1, b2,…, bn2,
n3 элементов k-ой группы x1, x2,…, xnk
можно составить ровно n1∙ n2∙…∙nk различных
упорядоченных комбинаций вида 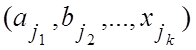 , содержащих по одному
элементу из каждой группы.
, содержащих по одному
элементу из каждой группы.
1. При k=2 утверждение выполняется (Лемма 1).
2.
Предположим, что Лемма 2
выполняется для k. Докажем для k+1 группы
элементов 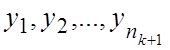 .
Рассмотрим комбинацию
.
Рассмотрим комбинацию 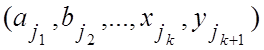 как
как ![]() и
и 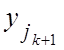 .
Предположение дает возможность вычислить число комбинаций из k
элементов, их n1 n2 nk. По Лемме 1 число комбинаций из k+1
элементов n1 n2… nk+1.
.
Предположение дает возможность вычислить число комбинаций из k
элементов, их n1 n2 nk. По Лемме 1 число комбинаций из k+1
элементов n1 n2… nk+1.
Пример. При бросании двух игральных костей N=6∙6=36. При бросании трех костей N=6∙6∙6=216.
Леммы 1 и 2 называются основными правилами комбинаторики.
Пусть имеется множество из n элементов a1, a2 ,an. Будем рассматривать выборку объема k 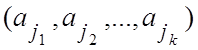 из n
элементов. Все выборки можно классифицировать по 2 признакам:
из n
элементов. Все выборки можно классифицировать по 2 признакам:
1. упорядоченные и неупорядоченные.
2. с возвращением и без возращения.
Если выборка упорядоченная, то выборки с одним и тем же составом выбранных элементов, но разным порядком элементов в выборках, считаются различными.
Если выборка считается неупорядоченной, то все выборки с одним и тем же составом элементов отождествляются.
Пример. Возьмем множество из трех элементов {1,2,3}. Выбираем k=2.
|
(1,1);(1,2);(1,3); (2,1);(2,2);(2,3); (3,1);(3,2);(3,3); |
(1,1);(1,2);(1,3); (2,2);(2,3); (3,3); |
С возвращением |
|
(1,2);(1,3); (2,1);(2,3); (3,1);(3,2); |
(1,2);(1,3); (2,3); |
Без возвращения |
|
упорядоченная |
неупорядоченная |
выборка |
Составим общую таблицу числа выборок:
|
|
|
С возвращением |
|
|
|
Без возвращения |
|
упорядоченная |
Неупорядоченная |
Выборка |
Упорядоченная выборка с возвращением ![]() ). Каждый элемент выборки может принимать n
значений, т.е. число выборок
). Каждый элемент выборки может принимать n
значений, т.е. число выборок 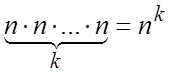 . Упорядоченная выборка
без возвращения
. Упорядоченная выборка
без возвращения ![]() .
.
o
Упорядоченная выборка без
возвращения называется размещением. Число размещений 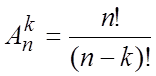 .
.
Пример. В лифт 12-этажного дома зашли 3 человека. Найти вероятность того, что все вышли на разных этажах.
![]() n=113.
n=113.
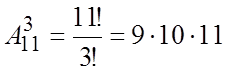 ,
, 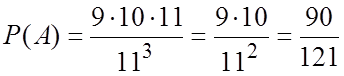 .
.
o Перестановкой из k элементов называется совокупность этих же элементов, записанных в произвольном порядке.
Pk-число перестановок из k элементов. 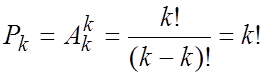 , поскольку 0!=1.
, поскольку 0!=1.
o
Произвольное k-элементное
подмножество множества n элементов называется сочетанием из n
элементов по k элементов. Сочетание—это неупорядоченная выборка
объема k из n элементов. Обозначается число всех сочетаний из n
элементов по k элементов через ![]() .
.
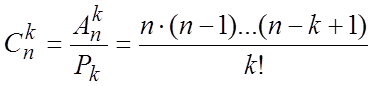 .
. 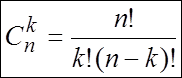 , где
, где ![]() .
.
![]() .
.
Свойства сочетаний:
1.
![]() .
.
2.
![]() .
.
3.
![]() .
.
4.
![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.