Точечные и интервальные оценки. Числовые характеристики выборки. Оценки параметров распределения. Методы получения точечных оценок

Задание 1.

В результате эксперимента получены две выборки  и  из генеральных совокупностей, записанные в виде статистических рядов.

            Требуется:

            1) записать значения результата эксперимента в виде вариационного ряда и интервального ряда;

            2) построить гистограмму частот и график эмпирической функции распределения.

            3) числовые характеристики выборок (среднее, мода, медиана, среднее квадратичное отклонение, дисперсия, коэффициенты эксцесса и асимметрии, размах вариации) с помощью программного продукта Excel;

            4) доверительные интервалы для математического ожидания при уровне надежности  95%.

            5) методами моментов и максимального правдоподобия оценить неизвестный параметр , считая что первая и вторая выборки произведены из генеральной совокупности соответственно с плотностями , ,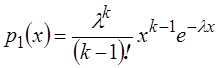

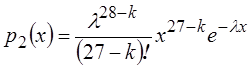, , где  - номер варианта.

X

21,1+k	17,2	50,4	22,6	21,1
17,2	20,5+k	16,9	18	19,7
19,5	23,1	18,6+k	19,4	20,1
21,3	22,6	21,1	20,3+k	21,3
22,4	17,2	19,8	19,5	16,8+k
35,7	32,5	46,8	20,3+k	72,5
42,3	46,8	18,9+k	67,6	64,8
56,5	16,1+k	37,8	71,4	54,1
14,6+k	37,8	54,1	66,2	23,5
29,2	17,2	58,2	46,8	50,4

Y

30,3	27,6	19,5	20,6	12,5+k
55,7	19,1	22,4	11,6+k	31,4
21,3	43,8	10,7+k	55,7	22,4
41,0	11,6+k	39,4	19,1	30,3
12,7+k	20,1	20,3	29,7	20,7
36,2	10,5+k	46,9	18,8	49,8
19,1	33,1	12,6+k	39,4	28,1
57,6	23,6	25,5	10,3+k	21,3
22,4	49,8	49,8	19,5	15,8+k
55,7	32,5	46,8	30,3	62,5

Здесь k – номер варианта.

ОПИСАТЕЛЬНАЯ СТАТИСТИКА

Среднее
Стандартная ошибка
Медиана
Мода	Значение варианты с наибольшей частотой
Стандартное отклонение
Дисперсия выборки
Эксцесс
Асимметричность
Интервал	Размах вариаций
Минимум	Минимальное значение выборки
Максимум	Максимальное значение выборки
Сумма
Счет	- объем выборки

ЛЕКЦИЯ 1.

ТОЧЕЧНЫЕ И ИНТЕРВАЛЬНЫЕ ОЦЕНКИ

1. БАЗОВЫЕ ПОНЯТИЯ СТАТИСТИКИ.. 3

1.1. Генеральная совокупность и выборка. 3

1.2. Способы представления и обработки статистических данных. 4

2.Числовые характеристики выборки. 5

3. Оценки параметров распределения. 7

3.1. Постановка задачи статистического оценивания неизвестных параметров распределения. 7

3.2. Виды оценок и их свойства. 7

3.3.Основные требования, предъявляемые к оценкам.. 7

4. Методы получения точечных оценок. 8

4.1. Метод моментов. 8

4.2. Метод максимального правдоподобия. 9

5. Интервальные оценки неизвестных параметров. 11

5.1. Доверительные интервалы для параметров распределения. 11

5.1.2. Доверительный интервал для дисперсии. 13

1. БАЗОВЫЕ ПОНЯТИЯ СТАТИСТИКИ

            При исследовании реальных процессов приходится обрабатывать большие объемы статистических данных по самым разнообразным показателям, которые по своей сути являются СВ. Часто возникает необходимость оценивания числовых значений различных параметров, неоднократно приходится выдвигать и проверять различные предположения, устанавливать наличие и силу зависимости между разнообразными факторами. На практике сталкиваемся с конкретными реализациями рассматриваемых СВ. Количество таких реализаций ограничено, что не позволяет применять напрямую теоретические методы анализа. Поэтому в первую очередь используются методы и модели математической статистики (в частности, выборочный метод), позволяющие получить необходимые знания об исследуемом объекте, осуществить направленный анализ и сделать обоснованные выводы.

            Одной из центральных задач математической статистики является выявление закономерностей в статистических данных, на базе которых можно строить соответствующие модели и принимать обдуманные решения. Под статистическими данными подразумеваются данные наблюдений за значениями некоторой СВ или совокупности СВ, характеризующих изучаемый процесс.