ЛЕКЦИЯ 6
ЗАКОН БОЛЬШИХ ЧИСЕЛ. ЦЕНТРАЛЬНАЯ ПРЕДЕЛЬНАЯ ТЕОРЕМА
6.1. Неравенство Чебышева. 1
6.2. Теорема Бернулли. Теорема Пуассона. 3
6.4. Центральная предельная теорема. 4
С давних времен замечены свойства устойчивости массовых явлений, а именно, при очень большом числе случайных явлений их средний результат практически перестает быть случайным и поэтому может быть предсказан с большой степенью точности. При этом конкретные особенности каждого отдельного случайного явления почти не сказываются на среднем результате таких явлений. Устойчивость средних характеристик в широком смысле называется законом больших чисел (ЗБЧ). ЗБЧ состоит из нескольких положений, главными из которых применительно к независимым случайным величинам являются: неравенство Чебышева, теорема Чебышева, теорема Бернулли, лемма Маркова и теорема Пуассона. Предельные теоремы дают возможность определить характер распределения суммы случайных величин при увеличении их числа.
Теорема 6.1. Для любой СВ x с дисперсией Dx и любого положительного e>0 справедливо неравенство:
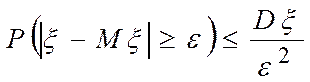 .
.
►Доказательство проведем для непрерывной случайной величины. Имеем
![]()
![]() .
.
Пусть x - непрерывная СВ. Тогда
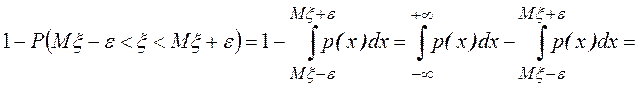
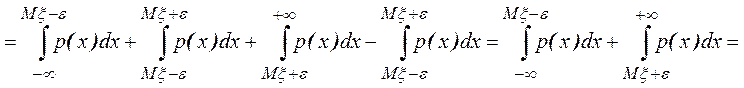
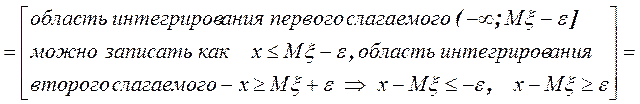
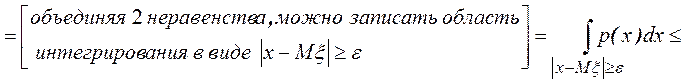
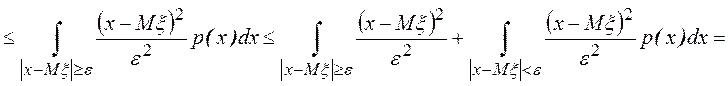
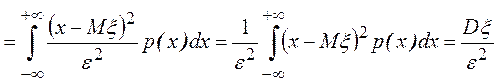 .
.
Аналогично доказывается, когда x - дискретная СВ. В этом случае знак ∫ заменяется на знак å.◄
Следствия.
1. Если ![]() , то
, то ![]() .
.
2. 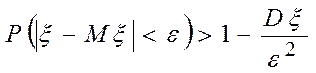 .
.
Первое следствие
подтверждает тот факт, что дисперсия характеризует отклонение значений ![]() от ее математического ожидания.. Чем ближе
дисперсия к нулю, тем более верно попадание всех значений
от ее математического ожидания.. Чем ближе
дисперсия к нулю, тем более верно попадание всех значений ![]() в очень малый интервал около ее
математического ожидания.
в очень малый интервал около ее
математического ожидания.
Пример. Вероятность отказа каждого из 10 приборов равна 0,01. Оценить вероятность того, что абсолютная величина разности между числом отказавших приборов и средним числом отказавших приборов меньше 2.
Решение.
Пусть x – число отказавших приборов
среди 10 приборов. Очевидно, что ![]() подчиняется
биномиальному закону распределения с параметрами
подчиняется
биномиальному закону распределения с параметрами ![]() ,
, ![]() ,
, ![]() .
Поэтому
.
Поэтому
![]() ,
, ![]() .
.
Тогда 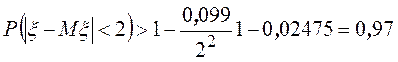 .
.
Теорема 6.2. (Чебышева) Пусть случайные величины x1, x2,…, xn попарно независимы с
математическими ожиданиями ![]() ,
, ![]() ,
, ![]() ,
, ![]() и дисперсиями
и дисперсиями ![]() ,
, ![]() ,
, ![]() ,
, ![]() , ограниченными одним и тем же числом
, ограниченными одним и тем же числом ![]() . Тогда для любого
. Тогда для любого ![]() :
:
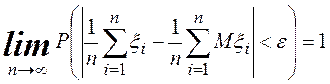 .
.
►Обозначим 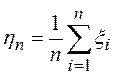 . Так как случайные величины
. Так как случайные величины ![]() независимы, то
независимы, то
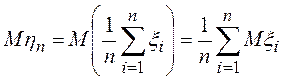 и
и
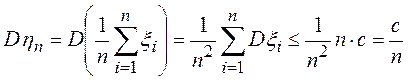 .
.
Применим к случайной величине ![]() неравенство Чебышева
неравенство Чебышева
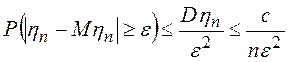 при
при ![]() .
.
Тогда ![]() при
при ![]() .
.
Подставляя вместо ![]() и
и ![]() соответствующие
выражения, получим соотношение
соответствующие
выражения, получим соотношение
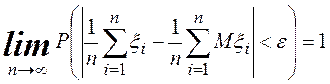 .◄
.◄
Следствие. 1. 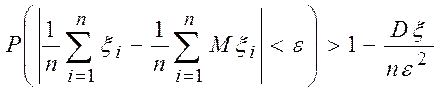
2. Если все случайные
величины ![]() ,
, ![]() ,
, ![]() ,
, ![]() одинаково
распределены и
одинаково
распределены и ![]() , то
, то
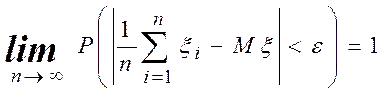 .
.
Пример. Сколько
раз нужно измерить величину, истинное значение которой равно ![]() , чтобы с вероятностью не меньшей 0,95
можно было утверждать, что среднее арифметическое этих значений отличается от
, чтобы с вероятностью не меньшей 0,95
можно было утверждать, что среднее арифметическое этих значений отличается от ![]() по абсолютной величине меньше, чем на 2,
если среднеквадратическое отклонение каждого измерения меньше 10.
по абсолютной величине меньше, чем на 2,
если среднеквадратическое отклонение каждого измерения меньше 10.
Решение.
По условию ![]() ,
, ![]() ,
, ![]() ,
, ![]() . Тогда
. Тогда
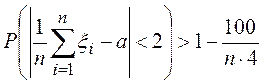 ,
, 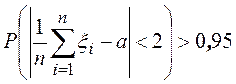 ,
,
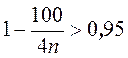 ,
, 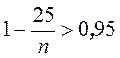 ,
,
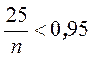 ,
, ![]() .
.
Теорема 6.3. (Маркова) Если СВ x принимает только положительные
значения, то вероятность того, что она примет какое - нибудь значение,
превосходящее положительное число ![]() , не больше, чем
, не больше, чем 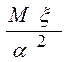 , равна
, равна
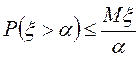 ,
, ![]() .
.
Следствие.
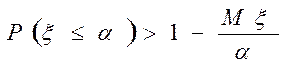
Пример. Оценить вероятность того, что в течение года в данной местности будет не более 220 солнечных дней, если среднее число солнечных дней в году – 100.
Решение. Пусть x - число солнечных дней в году для данной местности.
Мx = 100
a = 220
Р(x £ 220) > 1-100/1220 » 6/11 = 0,5.
Теорема 6.4. (Бернулли) Если в каждом из ![]() испытаний событие
испытаний событие ![]() появится
с вероятностью
появится
с вероятностью ![]() , то относительная частота
, то относительная частота ![]() сходится к
сходится к ![]() при
при ![]()
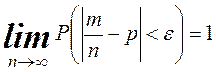 .
.
►Рассмотрим неравенство Чебышева для схемы независимых
испытаний Бернулли. Здесь ![]() число успехов. Тогда
число успехов. Тогда
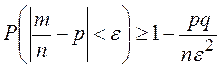 .
.
Переходя к пределу при ![]() ,
получим теорему Бернулли.◄
,
получим теорему Бернулли.◄
Следствие. 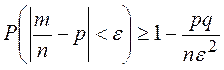 .
.
Пример. При штамповке пластинок из пластмассы по данным ОТК брак составляет 3%. Оценить вероятность того, что при просмотре партии в 10000 пластинок, выявится отклонение от установленного процента брака меньше, чем на 1%?
Решение.
![]() ,
, ![]() ,
, ![]() .
.
По теореме Бернулли имеем
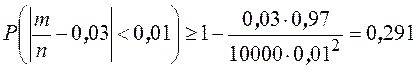 .
.
Теорема 6.5. (Пуассона) Если производится n независимых опытов и вероятность
появления события А в каждом опыте равна рk, то при увеличении n относительная частота ![]() сходится по вероятности к среднему
арифметическому вероятностей:
сходится по вероятности к среднему
арифметическому вероятностей:
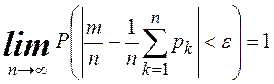 .
.
Теорема Бернулли и теорема Пуассона утверждают устойчивость частоты при постоянных условиях опыта.
ЗБЧ широко используются при решении практических задач. Свойство суммы случайных величин вести себя как неслучайная величина дает возможность прогнозировать результаты большинства массовых явлений.
Теорема
6.6. Пусть ![]() ,
, ![]() ,
, ![]() ,
, ![]() – независимые и одинаково распределенные
случайные величины,
– независимые и одинаково распределенные
случайные величины, ![]() ,
, ![]() ,
, ![]() ,
, 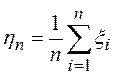 .
Тогда при
.
Тогда при ![]() равномерно по
равномерно по ![]() и
и ![]() имеем
имеем
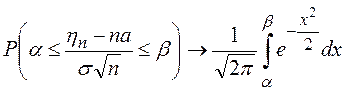 .
.
Центральная
предельная теорема устанавливает предельное распределение сумм большого числа
случайных величин, т.е. закон распределения случайной величины 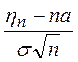 неограниченно приближается к нормальному
закону
неограниченно приближается к нормальному
закону ![]() .
.
Универсальность нормального закона распределения состоит в том, что при соответствующей нормировке последовательность независимых случайных величин стремится к нормальному закону.
Пример. Количество тонн цемента, взятое за день с цементного склада, является случайной величиной с рядом распределения
|
0 |
20 |
40 |
|
|
|
|
С какой вероятностью 2000 т цемента хватит на квартал (90 дней)?
Решение. Пусть ![]() – случайное количество цемента, взятое в
– случайное количество цемента, взятое в ![]() -й день со склада. Считаем, что эти
случайные величины независимы и одинаково распределены. Тогда
-й день со склада. Считаем, что эти
случайные величины независимы и одинаково распределены. Тогда ![]() ,
, ![]() .
Согласно теореме 6.6. закон распределения их суммы за квартал
.
Согласно теореме 6.6. закон распределения их суммы за квартал ![]() – приближенный нормальный с
параметрами
– приближенный нормальный с
параметрами ![]() ,
, ![]() ,
, ![]() .
.
Тогда
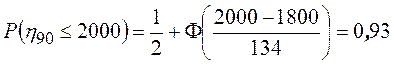 , где
, где 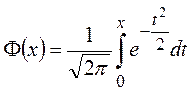 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.