Исследование взаимосвязи между выборками (Лабораторная работа № 3)

Лабораторная работа 3

ИССЛЕДОВАНИЕ ВЗАИМОСВЯЗИ МЕЖДУ ВЫБОРКАМИ

            Задание. Значения некоторого количественного признака  характеризуются значениями признака , где  и  – выборки из нормально распределенной двумерной генеральной совокупности. Требуется:

            1) составить ковариационную и корреляционную матрицы взаимосвязи  и ,

            2) найти уравнение линейной регрессии  на , имеющее вид ,

1.Статистическая и корреляционная зависимость

           При функциональной зависимости  каждому значению переменной  соответствует единственное значение . Для случайных величин и не всегда можно установить такую зависимость. Например, вес человека нельзя однозначно найти по его росту.

Между случайными величинами может существовать зависимость особого рода, при которой значения одной величины, например , влияют на закон распределения другой величины, .

Примерами такой зависимости является связь между валовым объемом продукции и себестоимостью выпускаемых изделий, между величиной урожая и количеством внесенных удобрений.

           Зависимость между случайными величинами и называется статистической, если каждому значению случайной величины соответствует определенный закон распределения случайной величины , а именно, если значению  соответствует закон распределения :

            1.1. Ковариационная матрица.

            При нахождении ковариационной матрицы используется статистический анализ Ковариация.

В таблице  приводятся формулы, по которым рассчитываются соответствующие значения.

Ковариационная матрица

	Столбец 1	Столбец 2
Столбец 1
Столбец 2

            Ковариационная матрица позволяет установить ассоциированы ли наборы данных по величине:

1) при  большим значениям выборки  соответствуют большие значения выборки ;

2) при  большим значениям выборки  соответствуют меньшие значения выборки  (или наоборот);

3)при  данные двух диапазонов не связаны.

            1.2. Корреляционная матрица

В таблице приводятся формулы, по которым рассчитываются соответствующие значения.

Таблица№№ Корреляционная матрица

	Столбец 1	Столбец 2
Столбец 1
Столбец 2

В таблице №№ 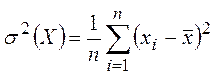 и .

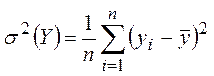            Корреляционная матрица также устанавливает ассоциированность наборов выборочных данных по величине:

1) при  большим значениям выборки  соответствуют большие значения выборки ;

2) при  большим значениям выборки  соответствуют меньшие значения выборки  (или наоборот);

3) при  данные двух диапазонов не коррелированы;

4) при  существует линейная функциональная зависимость между выборочными значениями  и .

            2. Уравнение линейной регрессии.

            Построение уравнения линейной  регрессии  на  ( регрессии  на ) проводится с помощью статистической функции ЛИНЕЙН

Коэффициент наклона к оси

Отрезок пересечения оси