ЛЕКЦИЯ 3
СХЕМА ИСПЫТАНИЙ БЕРНУЛЛИ
3.1. Повторные испытания в схеме Бернулли. 1
3.2. Рекуррентная формула для подсчета вероятностей в схеме Бернулли. 2
3.3.Наивероятнейшее число испытаний события в схеме Бернулли. 3
3.4. Приближенные формулы в схеме испытаний Бернулли. 4
3.5.Локальные теоремы Муавра-Лапласа. 5
3.6. Интегральная теорема Лапласа. 5
3.7. Отклонение относительной частоты от вероятности. 6
Повторные испытания независимы, если вероятность появления любого исхода в каждом испытании не зависит от реализации результатов в предыдущем испытании.
Определение 3.1. Схемой Бернулли – это выполнение следующих 3 условий:
1) производится n повторных испытаний,
2)
в каждом испытании возможно только 2 исхода: событие ![]() появилось
и событие
появилось
и событие ![]() не появилось,
не появилось,
3) вероятность появления события ![]() одинакова для каждого испытания и равна
одинакова для каждого испытания и равна ![]() :
:
![]() ,
, ![]() .
.
Примеры.
· Игральная кость бросается 5 раз:
![]() ,
, 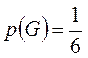 ,
, 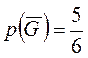
· Найти вероятность того, что при 3-х бросаниях монеты герб выпадет 2 раза:
W= {ГГГ, ГГР, ГРГ, РГГ, РГР, ГРР, РРР}
В = {выпало 2 герба и 1 решка}
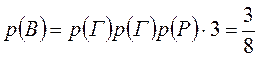 .
.
Теорема
3.1. Вероятность того, что в ![]() испытаниях схемы
Бернулли событие
испытаниях схемы
Бернулли событие ![]() произошло
произошло ![]() раз, вычисляется по формуле
раз, вычисляется по формуле
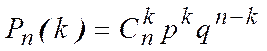 .
.
►Пусть ![]() – исход
– исход ![]() -того испытания.
-того испытания.
: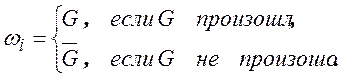
Тогда результатами испытания будут:
![]() ,
,
где событие ![]() произошло
произошло ![]() раз,
раз, ![]() произошло
произошло ![]() раз.
раз.
Тогда
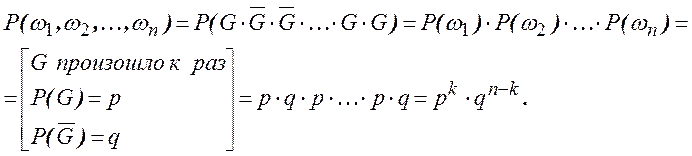
Вероятность события в ![]() испытаниях (событие
испытаниях (событие ![]() произошло
произошло ![]() раз) есть сумма стольких
элементарных событий {
раз) есть сумма стольких
элементарных событий {![]() – произошло
– произошло ![]() раз, `
раз, `![]() произошло
произошло
![]() ) раз}, сколько существует сочетаний из
) раз}, сколько существует сочетаний из ![]() элементов по
элементов по ![]() , т. е.
, т. е. ![]() .
.
Поэтому 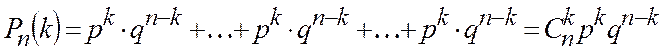 .◄
.◄
Примеры.
·
Завод
выпускает изделия, среди которых 5% - бракованные. Для проверки взято 5
деталей. Найти вероятности событий: ![]() ,
, ![]() .
.
Решение.
![]() ,
,
![]() ,
,
![]() ,
, ![]() .
.
Тогда ![]() ,
,
![]() .
.
· Завод изготавливает изделия, каждое из которых с вероятностью 0,05 может быть дефектным. Сколько деталей должно быть в партии, чтобы вероятность встретить в них хотя бы 1 дефектную деталь была не меньшей, чем 0,98.
Решение.
![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
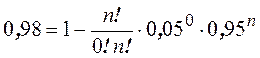 ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Теорема 3.2. 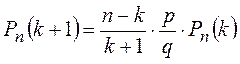 ,
, ![]() .
.
Пример. Найти распределение вероятностей числа бракованных деталей среди 5-ти отобранных, если вероятность брака 0,60.
Решение.
![]() ,
, ![]() =
{деталь бракованная}
=
{деталь бракованная}
р = 0,6, q = 0,4.
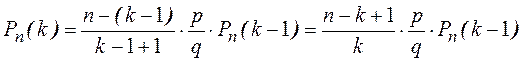
![]()
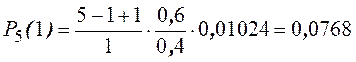
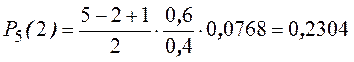
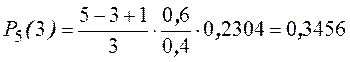
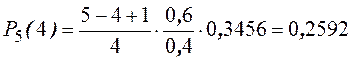
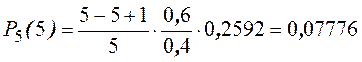
События Рn(0), Рn(1), …, Рn(n) составляют полную группу событий. Поэтому их сумма равна единице, т. е.
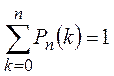 ,
,
![]() ,
,
![]() .
.
Если сравнить полученную формулу с формулой Бинома Ньютона
![]() .
.
Поэтому распределение вероятностей Рn(0), Рn(1), …, Рn(n) называется биноминальным распределением.
Определение 3.2. Наивероятнейшее
числоm0 появления события ![]() в
n независимых испытаниях – число, для которого вероятность Pn(m0) превышает или не меньше
вероятности каждого из возможных остальных исходов испытаний.
в
n независимых испытаниях – число, для которого вероятность Pn(m0) превышает или не меньше
вероятности каждого из возможных остальных исходов испытаний.
Теорема 3.3. ![]()
► По теореме 3.2. имеем:
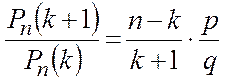 .
.
Согласно определению числа m0 имеем неравенства:
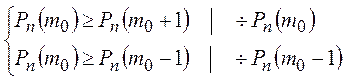
![]()
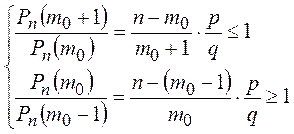
![]()
![]()
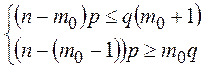
![]()
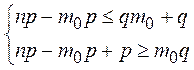
![]()
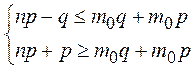
![]()
![]()
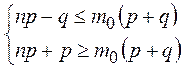
![]()
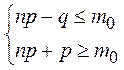
![]()
![]() ◄
◄
Пример. При данном технологическом процессе 85% произведенной продукции высшего качества. Найти наивероятнейшее число изделий высшего сорта в партии из 120 изделий.
Решение.
n = 120, ![]() = {изделия высшего сорта},
р = 0,85, q = 0,15
= {изделия высшего сорта},
р = 0,85, q = 0,15
120*0,85 – 0,15≤m0≤120*0,85 + 0,85
101,85≤m0≤102,85
m0 = 102
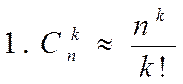
По определению:
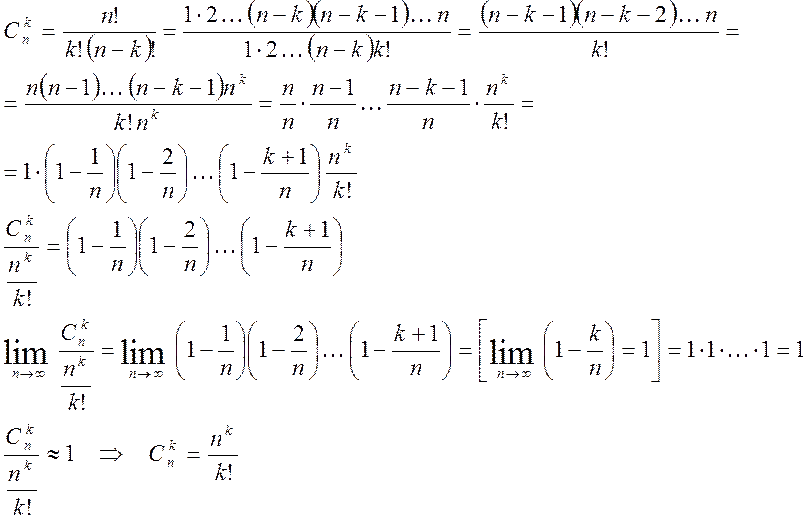
Теорема3.4. (Пуассона) Если в схеме испытаний Бернулли
![]() – велико,
– велико, ![]() – мало,
– мало,
![]() – конечное число, то справедлива формула
Пуассона:
– конечное число, то справедлива формула
Пуассона:
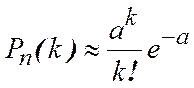 .
.
► По формуле Бернулли
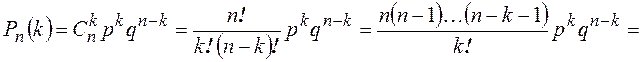
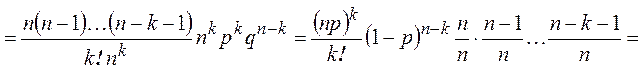
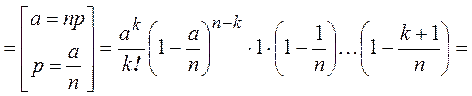
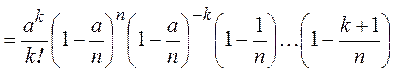
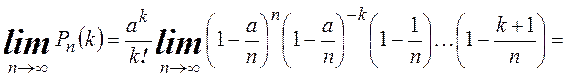
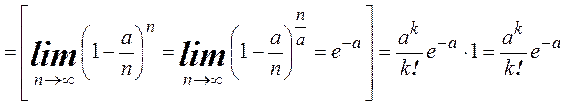 .◄
.◄
Пример. Прибор содержит тысячу элементов. Вероятность выхода из строя каждого элемента 0,002. Найти вероятность того, что из строя вышло не более 7 элементов.
Решение.
n=1000,р = 0,002,к£7
![]() = 1000*0,002 = 2
= 1000*0,002 = 2
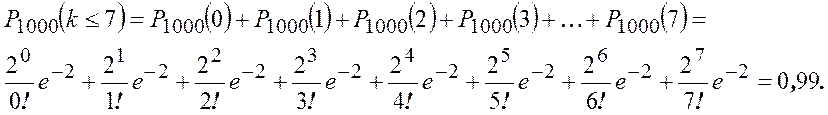
Теорема 3.5. Если в схеме испытаний Бернулли число испытаний ![]() велико,
велико, ![]() , число
, число 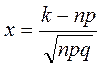 ограничено, то вероятность
того, что в
ограничено, то вероятность
того, что в ![]() испытаниях событие
испытаниях событие ![]() произойдет
произойдет
![]() раз, находится по формуле
раз, находится по формуле 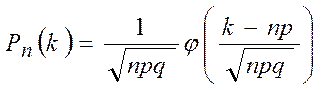 , где
, где 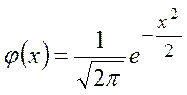 -
функция Лапласа.
-
функция Лапласа.
Функция Лапласа вычисляется по специальным таблицам. Для того чтобы уметь пользоваться таблицами, надо знать свойства функции j(х):
1. График функции:
2. Функция ![]() является четной,
поэтому таблицы составлены только для положительных значений
является четной,
поэтому таблицы составлены только для положительных значений![]() .
.
3. Ось ![]() является асимптотой
графика функции
является асимптотой
графика функции ![]() и к ней достаточно быстро
приближаются ветви графика. Поэтому таблицы составлены для значений х от 0 до
4. Если надо найти значение j(х), х>4, то берут последнее табличное значение.
и к ней достаточно быстро
приближаются ветви графика. Поэтому таблицы составлены для значений х от 0 до
4. Если надо найти значение j(х), х>4, то берут последнее табличное значение.
Пример. По данным ОТК 80% всей продукции, выпускаемой заводом, стандартны. Найти вероятность того, что среди взятых 400 изделий бракованными будут 40.
Решение.
![]() = {1 изделие бракованное}, n =
400, р = 0,2, к = 40
= {1 изделие бракованное}, n =
400, р = 0,2, к = 40
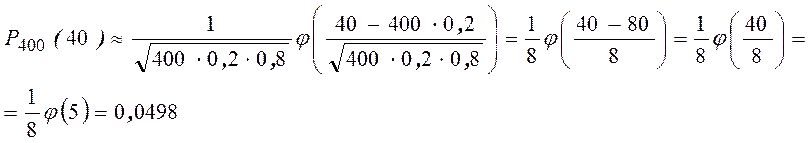
Теорема 3.6. Если в схеме испытаний Бернулли n – велико,
0<р<1, то вероятность того, что в n испытаниях событие А произойдет не
менее к1 раз и не более к2 раз, удовлетворяет
соотношению: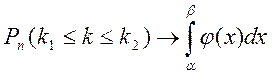 , где
, где 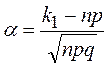 и
и 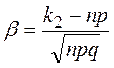 .
.
Преобразуем формулу:
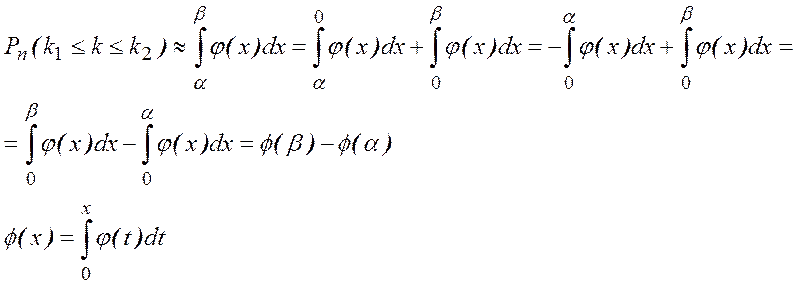
Поэтому интегральную формулу Муавра – Лапласа можно записать в виде
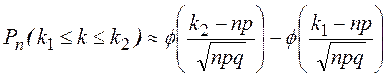 ,
,
где 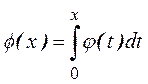 .
.
Значения функции f(х) находятся в таблицах.
Свойства функции f(x):
1. График функции:
2. f(х) – функция нечетная, поэтому таблицы приведены только для положительных значений х.
3. График функции имеет 2 асимптоты у1 = 0,5 и у2 = -0,5, к которой быстро приближаются, поэтому таблицы составлены для значений х от 0 до 4. При х>4 берется последнее значение таблицы.
Пример. Промышленная телевизионная установка содержит 2000 транзисторов. Вероятность выхода из строя каждого из транзисторов – 0,0005. Найти вероятность выхода из строя от 50 до 60 транзисторов.
Решение.
50£к£60, n = 2000, р = 0,0005
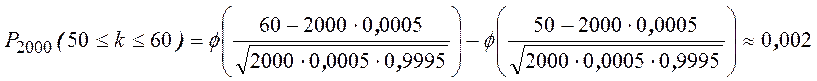 .
.
Относительная частота ![]() появления события
появления события ![]() в
в
![]() испытаниях
испытаниях 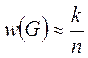 .
.
При ![]() относительная частота
стремится к вероятности события
относительная частота
стремится к вероятности события ![]() . Тогда
. Тогда 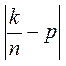 – абсолютное отклонение относительной
частоты от вероятности.
– абсолютное отклонение относительной
частоты от вероятности.
Теорема 3.7. 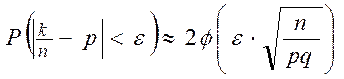
►Пусть дано ![]() . Тогда:
. Тогда:
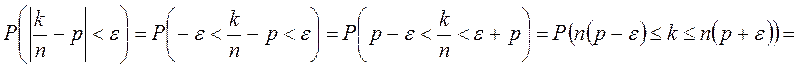
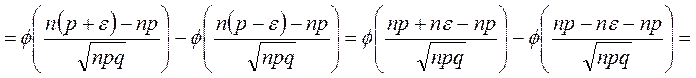
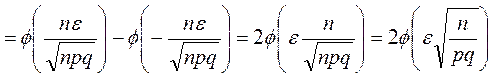 ◄
◄
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.