Непосредственно перед выполнением практикума нужно провести с учениками вводную беседу о задачах практикума, его содержании, об организации и графике выполнения работ, специальных правилах поведения во время занятий; в этой беседе следует дать анализ каждой работы с указанием специфических условий ее выполнения и специальных правил техники безопасности; рассказать о приемах измерений и правилах пользования измерительными приборами, об анализе погрешностей и приближенных вычислениях, форме отчета и сроке его сдачи учителю. В заключение нужно разделить учащихся на звенья (в случае необходимости – на подгруппы), раздать им согласно графику инструкции к следующей работе и указать дальнейший порядок обмена инструкциями между звеньями, объяснить, как следует готовиться дома к работе и каковы требования при допуске к ее выполнению. (Поскольку среди учащихся будут такие, которые не успеют выполнить работу за отведенное на нее время, желательно, чтобы практикум по физике проводился на последних уроках.)
Содержание отчета о выполненной работе практикума (оформляемого в специальной тетради) должны составлять схематический рисунок установки, с помощью которой был осуществлён эксперимент, описание хода опытов, результаты наблюдений и измерений, обработка данных эксперимента (вычищение средних значений величин погрешностей, заполнение таблиц, построение графиков, запись конечного результата). В него включаются также описание дополнительных заданий и ответы на контрольные вопросы (такие сведения из инструкции, как перечень приборов и материалов, описание устройства приборов, примечание к правкам их эксплуатации и т.п., повторять в отчете нецелесообразно, так как они не отражают понимания школьниками сущности выполненного эксперимента.)
II.ПРИБЛИЖЕННЫЕ ВЫЧИСЛЕНИЯ В КУРСЕ СРЕДНЕЙ ШКОЛЫ.
Разность между приближенным значением xизм и точным xист
![]()
характеризует отклонение полученного результата от истинного значения искомой величины и называется абсолютной погрешностью измерения.
Максимальная абсолютная погрешность Δx является верхней границей погрешности |δx|.Она определяется неравенством
![]()
и принимается за количественную оценку точности измерения.
С целью упрощения терминологии величину Δx принято называть абсолютной погрешностью измерения или просто погрешностью, понимая под этим модуль границы абсолютной погрешности.
Результат измерения записывают в следующей форме
![]()
Приведенная форма записи приближенных чисел называется интервальной.
Для определения и сравнения точности измерений используют относительную погрешность – отношение абсолютной погрешнос-ти к значению измеряемой величины:
ε =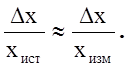
Значащими цифрами числа называются все его цифры, в том числе и нули, если они не расположены в начале числа.
Цифра приближенного числа называется верной, если его абсолютная погрешность не превышает одной единицы того разряда, в котором стоит данная цифра. Например, в приближенном числе 46±2 абсолютная погрешность 2 не превышает одного десятка (2<10) но превышает одну единицу (2>1). Поэтому в приведенном приближенном числе цифра 4, стоящая в разряде десятков, является верной, а о цифре 6, стоящей в разряде единиц, этого сказать нельзя. Цифра, стоящая за последней верной, является не вполне точно определенной: в ней содержится погрешность, поэтому она называется сомнительной. Цифры приближенного числа, стоящие после сомнительной, неверные. Действительно, так как сомнительная цифра не может быть определена точно, то цифры последующих более младших разрядов невозможно найти и даже оценить. Поэтому неверные цифры, как не содержащие реальной информации, бессмысленны и должны быть отброшены. Например, в приближенном числе 307,25±4 пять значащих цифр 3,0, 7, 2, 5. Из них две первые 3 и 0 – верные, третья цифра 7 – сомнительная, а две последние 2 и 5 – неверные. Значит, правильной будет запись 307±4. В случае приближенного числа 120,385±0,5 следует писать 120,4±0,5. По той же причине для числа 48,02±0,3 грамотной будет запись 48,0±0,3. Во всех случаях в последнем разряде приближенного числа стоит сомнительная цифра, неверных цифр нет.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.