Исследование цепей синусоидального тока (Лабораторная работа № 4), страница 5

            Резонансные кривые были построены здесь в зависимости от относительной расстройки частоты. Можно вывести расчетные выражения и построить резонансные кривые в зависимости от ω или относительной частоты. Следует отметить, что максимумы резонансных кривых на рисунке 13 равны, так как на оси ординат отложено отношение токов. Если откладывать ток I, то при разных R максимумы резонансных кривых не совпадут в одной точке.

            Полосу частот близи резонанса, на границах которой ток снижается до 0,707 резонансного значения, принято называть полосой пропускания резонансного контура. При токе 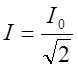  мощность, расходуемая в сопротивлении R равна:

,

т.е. составляет половину мощности, расходуемой при резонансе поэтому полосу пропускания характеризуют как полосу, границы которой соответствуют половине максимальной мощности. На границе полосы пропускания резонансного контура активное и реактивное сопротивления равны по величине. Это следует из условия

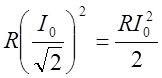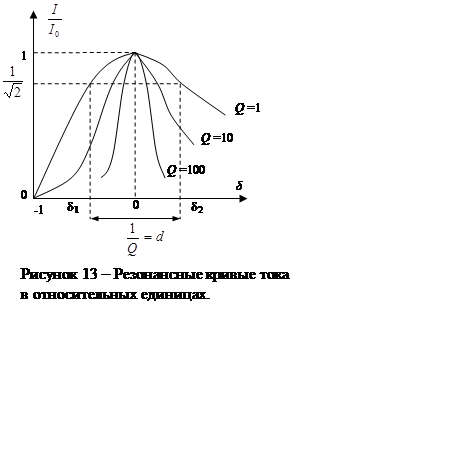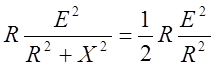
Соответственно и фазовый сдвиг между напряжением на зажимах цепи и током составляет 45º; на нижней границе комплексное сопротивление цепи имеет емкостной характер (ток опережает напряжение); на верхней границе комплексное сопротивление цепи имеет индуктивный характер (ток отстает от напряжения).

Условие для границы полосы пропускания записывается:

  или 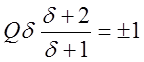 , откуда  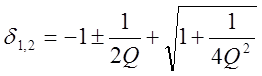4.9

По определению полоса пропускания резонансного контура находится из условия

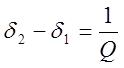 или  .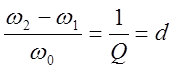

Величина d называется затуханием контура.

            В радиотехнических устройствах к одному из реактивных элементов колебательного контура, например емкости, подключается нагрузка в виде сопротивления . Вследствие этого возрастают потери в цепи и соответственно уменьшается добротность. Для определения добротности нагруженного контура параллельное соединениеи С может быть заменено эквивалентным при резонансной частоте последовательным соединением емкости и «вносимого сопротивления» . С этой целью используются условия эквивалентности цепей с последовательным и параллельным соединениями. Добротность нагруженного контура равна

 , а затухание увеличивается на величину вносимого затухания

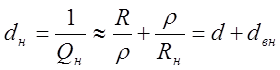
Если вносимое сопротивление значительно превышает сопротивление R, то

.

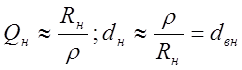Внутреннее сопротивление источника напряжения R_i  , добавляемое к сопротивлению R влияет на добротность и полосу пропускания колебательного контура: чем больше   R_i  тем ниже добротность и шире полоса пропускания контура. Поэтому с точки зрения сокращения полосы пропускания последовательного колебательного контура выгоден источник напряжения с малым внутренним сопротивлением.

            В условиях близких к резонансу, напряжения на индуктивности и емкости могут быть очень велики, что необходимо учитывать во избежание повреждения изоляции.

На рисунке 14 показана векторная диаграмма тока и напряжений при резонансе. Напряжения на реактивных элементах при резонансе определяются из выражения

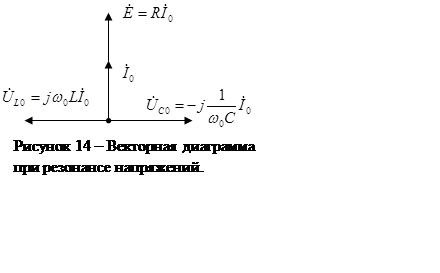
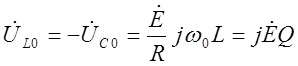    4.11.

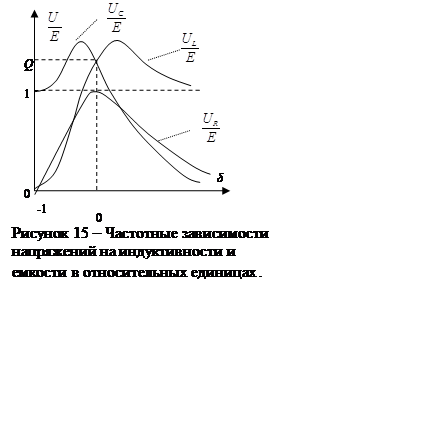
При Q>1 эти напряжения превышают по величине напряжение U=E, приложенное к резонансному контуру. Однако значения, получаемые на основании 4.11, не являются максимальными: максимум напряже-ния располагается несколько выше (правее), а максимум – ниже (правее) резонансной частоты (рис.15).

            Напряжение на индуктивности , равное нулю при ω = 0 , с увеличением ω может возрастать только до тех пор, пока ток не начнет снижаться быстрее, чем возрастает ω. После этого  спадает, стремясь в пределе к Е . Напряжение на емкости 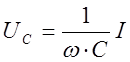, равное при ω = 0 приложенному напряжению U=E увеличивается, пока ток растет быстрее чем  ω, затем  спадает, стремясь в пределе к нулю. Кривые  и  пересекаются при резонансе, причем ордината точки пересечения в соответствие с 4.11 равна QE .

            Возвращаясь к определению понятия добротности рассматриваемой резонансной цепи, видно, что наряду с формулами 4.3 и 4.4 добротность цепи характеризуется выражениями 4.10 и 4.11, а именно:

.

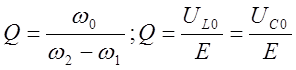Последняя формула показывает, что добротность исследуемой цепи определяется как кратность перенапряжения на L и C при резонансной частоте.

      1.5 Параллельный колебательный контур