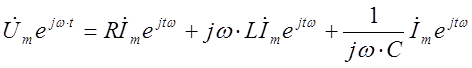Исследование цепей синусоидального тока (Лабораторная работа № 4), страница 3

     3.2

Здесь следует обратить внимание на то, что при интегрировании функции      постоянная интегрирования опущена, так как в рассматриваемом установившемся режиме цепи синусоидального тока электрические заряды и напряжения на емкостях представляют собой синусоидальные функции, не содержащие постоянных слагающих. В результате сокращения всех частей уравнения на множитель  получается алгебраическое комплексное уравнение

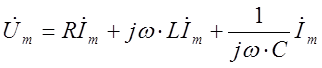
Ток выносим за скобки и вводим обозначение для комплексного сопротивления:

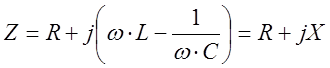   3.3

Таким образом получаем уравнение

   3.4 ,

 выражающее закон Ома для комплексных амплитуд.

Разделив обе части уравнения 3.4 на    получим закон Ома для комплексных действующих значений:

   3.5

Комплексное сопротивление Z представлено в выражении 3.3  в алгебраической форме. Та же величина в тригонометрической и показательной (полярной ) форме имеет вид:

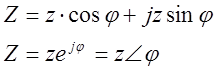  3.6

здесь  -- модуль комплексного числа Z – представляет собой полное сопротивление цепи, а φ – аргумент комплексного числа Z:

.

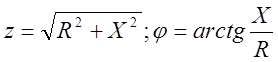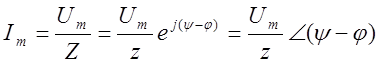На основании 3.4 комплексная амплитуда тока , где ψ-φ - начальная фаза тока. Искомый ток в тригонометрической форме :

.

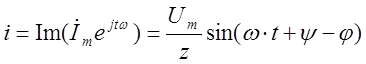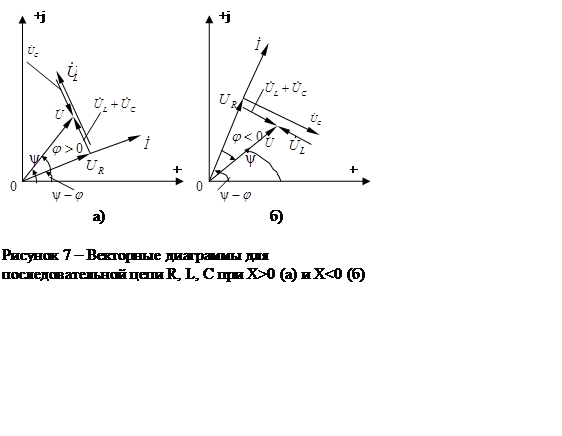
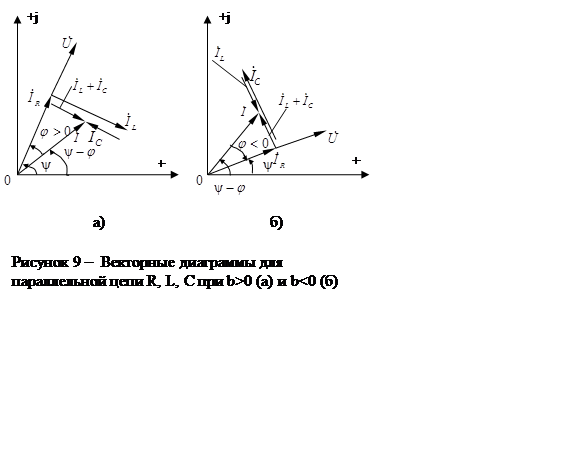
На рисунке 7 дана геометрическая интерпретация на комплексной плоскости уравнения 3.5.

Как видно из векторных диаграмм, приведенных на рисунке 7 напряжение на сопротивлении R совпадает по фазе с током ; напряжение на индуктивности опережает , а напряжение на емкости отстает от тока на угол . Геометрическая сумма векторов  дает вектор приложенного к цепи напряжения .

Прямоугольный треугольник, катетами которого являются , а гипотенуза которого равнаназывается треугольником напряжений. Если все стороны векторы этого треугольника разделить на вектор, то получится треугольник сопротивлений (рисунке 8), подобный треугольнику напряжений и повернутый относительно последнего на угол  по ходу часовой стрелки. 

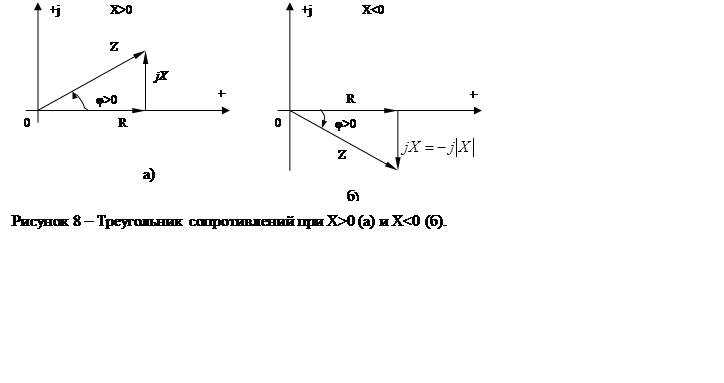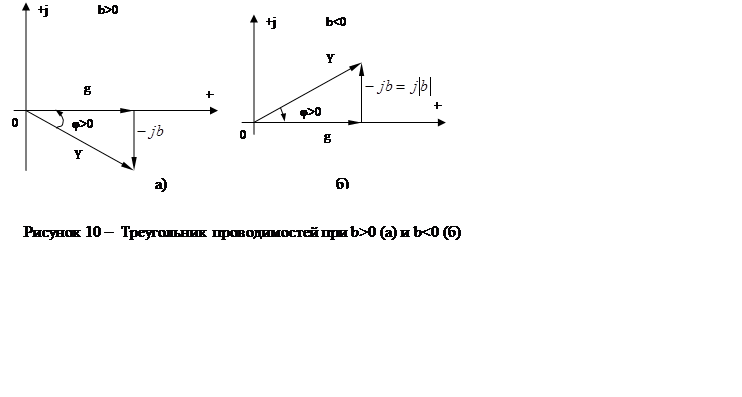
Треугольник сопротивлений представляет собой геометрическую интерпретацию уравнения 3.6. Его положение не зависит от начальных фаз  и ; сопротивление R откладывается на комплексной плоскости в положительном направлении действительной оси, а реактивное сопротивление Х в зависимости от его знака откладывается в положительном или отрицательном направлении мнимой оси. В треугольнике сопротивлений угол отсчитывается от катета R к гипотенузе Z по аналогии с тем, как отсчитывается угол в треугольнике напряжений от  к .   

1.3.2 Параллельное соединение R, L, C

Аналогично рассмотренному выше приходим к комплексной форме законов Ома и Кирхгофа для электрической цепи, состоящей из параллельно соединенных элементов.

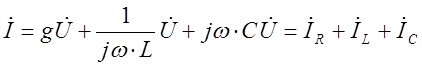   3.7

здесь  - ток в сопротивлении R (совпадает по фазе с напряжением ); 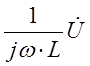- ток в индуктивности (отстает от напряжения на );   - ток в емкости (опережает напряжение на  ).

Выражение

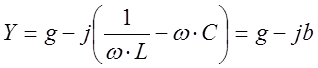  3.8

представляет собой комплексную проводимость цепи; g и b активная и реактивная проводимости цепи.

Закон Ома в комплексной форме:

. 3.9

Комплексная проводимость в тригонометрической и показательной (полярной ) форме имеет вид:   

 - полная проводимость цепи;

комплексный и синусоидальный ток соответственно равны:

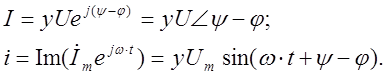3.10

На рисунке 9 дана геометрическая интерпретация на комплексной плоскости уравнения 3.7. прямоугольный треугольник с катетами   и  и гипотенузой  называется треугольником токов. Если все стороны векторы этого треугольника разделить на вектор , то получится треугольник проводимостей (рисунке 10), подобный треугольнику токов и повернутый относительно последнего на угол по ходу часовой стрелки. Активная проводимость g откладывается на комплексной плоскости в положительном направлении действительной оси, а реактивная проводимость b в зависимости от её знака откладывается в отрицательном (b>0) или положительном (b<0) направлении мнимой оси. Угол отсчитывается от гипотенузы Y к катету g по аналогии с треугольником токов, где угол отсчитывается от к  .

1.3.3 Зависимость между сопротивлениями и проводимостями участка цепи

Пользуясь комплексной формой записи , при заданном комплексном сопротивлении Z=R+jX некоторого участка цепи находим для того же участка комплексную проводимость: