Исследование цепей синусоидального тока (Лабораторная работа № 4)

Лабораторная работа №4

Исследование цепей синусоидального тока

    Цель работы:

- усвоить основные понятия и величины, характеризующие электрические цепи однофазного синусоидального тока;

- изучить особенности применения правил Кирхгофа для расчёта цепей однофазного синусоидального тока;

- усвоить основы символического метода расчёта цепей однофазного синусоидального тока (методом комплексных амплитуд);

- научиться строить векторные диаграммы, а также треугольники сопротивлений, проводимостей и мощностей;

- ознакомиться с резонансным явлением в колебательных контурах, с селективными свойствами контуров;

- приобрести навыки по расчёту и измерению синусоидальных напряжений и токов, параметров колебательных контуров.

Продолжительность работы 4 часа.

      1 Сведения из теории

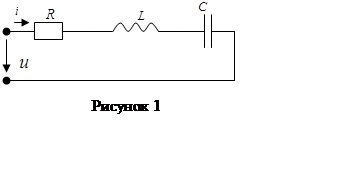
      1.1 Последовательное соединение.

При  прохождении синусоидального тока через электрическую цепь, состо-ящую из последовательно соединённых элементов R, L и C (рисунке 1)  на зажимах этой цепи со-здается синусоидальное напряжение, равное алгебраической сумме синусоидальных напря-жений на отдельных элементах (второй закон Кирхгофа):

           

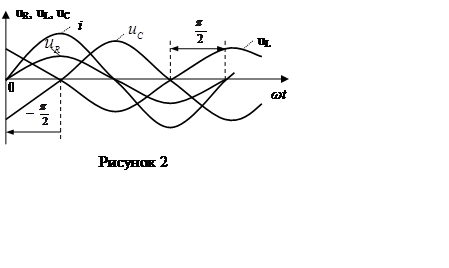Напряжение  на сопротивлении Rсовпадает по фазе с током  i напряжение  на индуктивности L  опережает , а напряжение  на емкости C отстает по фазе от i на  (рисунке 2) . Следовательно напряжение Uна зажимах всей цепи равно:

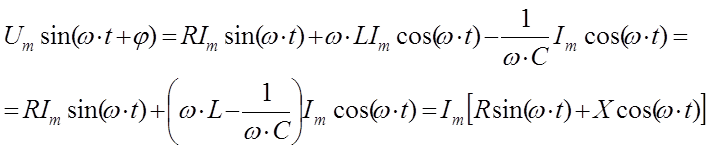  (1.1)

Уравнение 1.1 представляет тригонометрическую форму  записи второго правилА Кирхгофа для мгновенных значений напряжений. Входящая в него величина 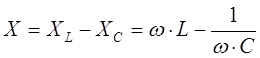  называется реактивным сопротивлением цепи, которое в зависимости от знака может иметь индуктивный (X>0) или емкостной (X<0) характер.

В отличие от реактивного сопротивления X величина активного сопротивления R всегда положительна.

Для нахождения U_mи  φ  воспользуемся тригонометрическими соотношениями:

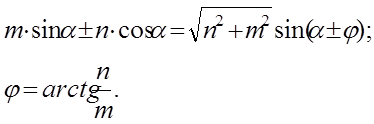(1.2)

Итак,    

         (1.3)

    

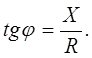
(1.4)

Выражение 1.3 показывает, что амплитуды и действующие значения напряжения на зажимах цепи и тока, проходящего через данную цепь, связаны отношением, аналогичным закону Ома:

где 

               (1.5)

называется полным сопротивлением рассматриваемой цепи.

Активное, реактивное и полное сопротивления относятся к числу основных понятий, применяемых в теории электрических цепей.

Выражения 1.1 и 1.4 показывают, что ток i отстаёт от напряжения Uна угол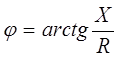

Если задано напряжение   на зажимах цепи с последовательно соединёнными R,L и C , то ток определяется по формуле:

.

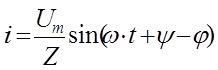Угол φ, равный разности начальных фаз напряжения и тока, отсчитывается по оси ωtв направлении от напряжения к току и бывает острым или прямым:

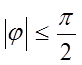
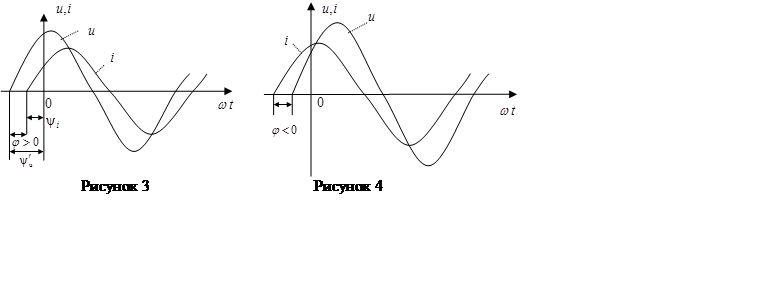
Угол φ положителен при индуктивном характере цепи (X>0) при этом ток отстает по фазе от напряжения и φ отсчитывается по оси абсцисс вправо от напряжения к току (рисунок 3).

Угол φ отрицателен при емкостном характере цепи (X<0) при этом ток опережает по фазе  напряжение и φ отсчитывается по оси абсцисс влево от напряжения к току (рисунок 4).

Ток совпадает с напряжением по фазе при , т.е. при равенстве индуктивного и емкостного сопротивлений. Такой режим работы электрической цепи называется резонансом напряжений. Из выражений 1.4 и 1.5 следует , что активное и реактивное сопротивления цепи связаны с полным сопротивлением формулами :

                                               (1.6)

Умножив правые и левые части выражений 1.6 на действующее значение тока I получим действующее значение напряжений на активном и реактивном сопротивлениях, называемые активной и реактивной составляющими напряжения:

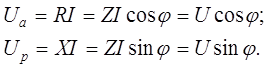    (1.7)

Мгновенные значения напряжений на активном и реактивном сопротивлениях , суммирующиеся алгебраически  в соответствии с 1.1 имеют фазовый сдвиг .

Поэтому непосредственное сложение действующих значений этих функций не дает действующего значения напряжения во всей цепи: согласно 1.7 активная и реактивная составляющие напряжения связаны с действующим значением суммарного напряжения формулой:

.

Для характеристики индуктивных катушек, представляемых цепью с последовательным соединением элементов R и L пользуются понятием добротности катушки 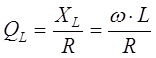, которое равнозначно тангенсу угла сдвига фаз φ для катушки. Чем меньше сопротивление R тем выше при прочих равных условиях добротность катушки. Добротность индуктивных катушек , применяемых в радиотехнике, автоматике и приборостроении обычно не превышает . Для достижения более высокой добротности применяются так называемые пьезоэлектрические резонаторы. 

1.2 Параллельное соединение

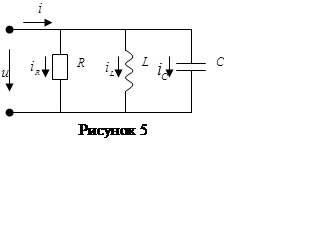
Если к зажимам электрической цепи, состоящей из параллельно соединенных элементов R, L и C (рисунок 5) приложено синусоидальное напряжение , то синусоидальный ток, проходящий через эту цепь равен алгебраической сумме синусоидальных токов в параллельных ветвях (первый закон Кирхгофа)  .