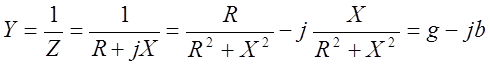 3.11
3.11
Если задана комплексная проводимость Y=g-jb некоторого участка цепи то комплексное сопротивление того же участка равно:
![]()
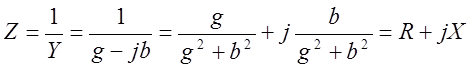 3.12
3.12
Выражения 3.11 и 3.12 показывают, что реактивное сопротивление X и реактивная проводимость b одного и того же участка цепи имеют одинаковый знак. Кроме того каждая слагающая проводимости (g и b) зависит как от активного, так и от реактивного сопротивлений.
Соотношения 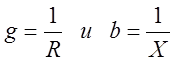 справедливы
только в частном случае, когда элемент R, L или
C рассматриваются в отдельности, например:
справедливы
только в частном случае, когда элемент R, L или
C рассматриваются в отдельности, например:
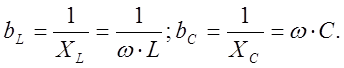
1.4 Последовательный колебательный контур
1.4.1 Резонанс напряжений
 Резонансная цепь с последовательным соединением является простейшей
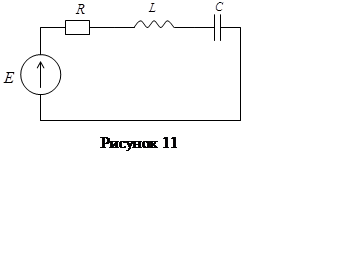
цепью для изучения явления резонанса напряжений (рис.11). Комплексное
сопротивление такой цепи зависит от частоты:
Резонансная цепь с последовательным соединением является простейшей
цепью для изучения явления резонанса напряжений (рис.11). Комплексное
сопротивление такой цепи зависит от частоты:
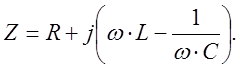 4.1
4.1
Резонанс напряжений наступает при частоте ω0
, когда 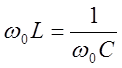 ; отсюда
; отсюда
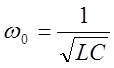 4.2
4.2
Мгновенные значения энергии выражаются формулами:
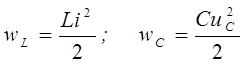
Если принять ![]() , то
, то ![]() . Поэтому
. Поэтому
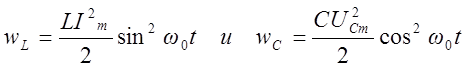 .
.
Максимальные значения этих энергий равны друг другу, так как
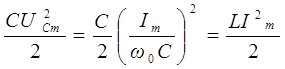
Это следует из того, что реактивное сопротивление цепи, содержащей индуктивность и ёмкость, при любой схеме соединений пропорционально разности максимальных значений энергий, запасаемой в магнитном и электрическом полях:
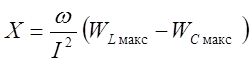 .
.
Поэтому условию резонанса (Х=0) соответствует равенство:
![]() .
.
Мгновенные значения ![]() и
и ![]() колеблются с удвоенной частотой около среднего значения
колеблются с удвоенной частотой около среднего значения 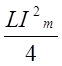 причем
происходит непрерывное перераспределение энергии магнитного и электрического
полей, суммарное значение которой постоянно:
причем
происходит непрерывное перераспределение энергии магнитного и электрического
полей, суммарное значение которой постоянно:
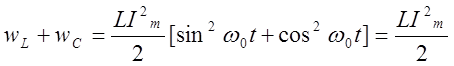 .
.
В рассматриваемом случае (резонанс напряжений ) в цепи не происходит обмена энергии между источником и реактивными элементами цепи, а вся электрическая энергия, поступающая от источника, расходуется в сопротивлении R.
Известно, что добротность индуктивной катушки и конденсатора равны соответственно:
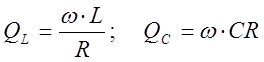 . Умножив и разделив
выражение для
. Умножив и разделив
выражение для ![]() на
на
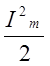 ,
получим:
,
получим:
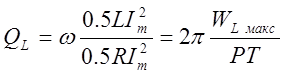
Здесь ![]() - максимум энергии, периодически запасаемой
индуктивностью L; P – средняя мощность, расходуемая в сопротивлении при
амплитуде тока
- максимум энергии, периодически запасаемой
индуктивностью L; P – средняя мощность, расходуемая в сопротивлении при
амплитуде тока ![]() .
.
Аналогично, разделив ![]() на
на 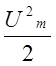 получим:
получим:
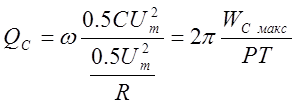
Здесь ![]() - максимум энергии, периодически запасаемой ёмкостью С; P –
средняя мощность потерь в параллельном сопротивлении R при амплитуде
напряжения на ёмкости
- максимум энергии, периодически запасаемой ёмкостью С; P –
средняя мощность потерь в параллельном сопротивлении R при амплитуде
напряжения на ёмкости ![]() .
.
Следовательно в обоих случаях добротность определяется в зависимости от отношения максимума энергии реактивного элемента к энергии РТ, выделяемой в виде тепла за период.
В случае резонансной цепи также пользуются понятием добротности цепи, подразумевая под этим в общем случае величину:
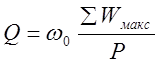 4.3
4.3
Здесь ω0 - резонансная частота, ![]() - сумма максимальных значений энергии
периодически запасаемой при резонансе в индуктивных (или емкостных) элементах,
Р – активная мощность на зажимах цепи при резонансе.
- сумма максимальных значений энергии
периодически запасаемой при резонансе в индуктивных (или емкостных) элементах,
Р – активная мощность на зажимах цепи при резонансе.
Для схемы рисунок 11 на основании 4.3 получаем:
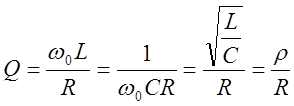 , 4.4
, 4.4
где 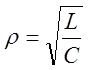
называется характеристическим (или волновым) сопротивлением резонансного контура.
Условимся называть относительной расстройкой частоты по отношению к резонансной частоте контура величину
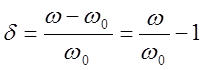 4.5
4.5
Сопротивление контура согласно 4.1 и с учетом 4.2 и 4.4
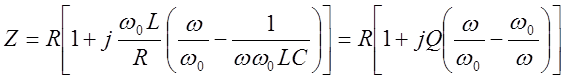
откуда используя 4.5, 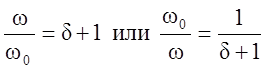 ,
получаем
,
получаем 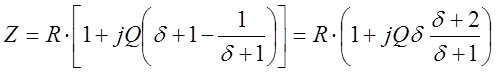 4.6
4.6
Следовательно, полное сопротивление цепи
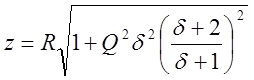 и
угол
и
угол 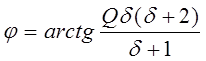
Ток в цепи
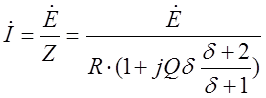
При частоте, близкой к резонансной, величина δ значительно меньше единицы и поэтому приближенно
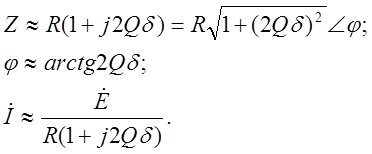 4.7
4.7
Выражения 5.7 практически достаточно
точны при ![]() . При
. При ![]() погрешность в сопротивлении z меньше 10 %.
погрешность в сопротивлении z меньше 10 %.
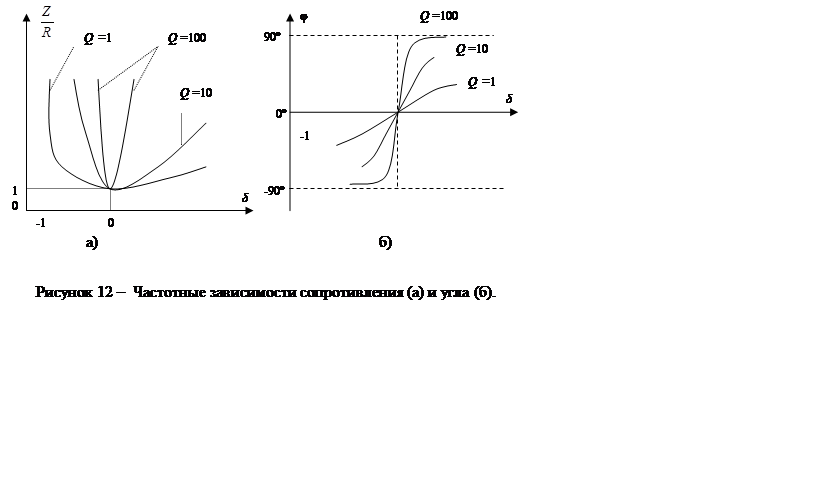
На рисунке 12 кривые даны в относительных единицах. Полное сопротивление цепи минимально при резонансе напряжений, при этом ток в цепи достигает своего максимального значения.
 |
На рисунке 13резонансные кривые тока в относительных единицах. По оси ординат отложены значения отношения токов к максимальному току при резонансе:
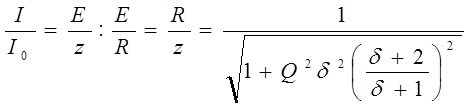 4.8
4.8
Чем выше добротность цепи Q , тем острее резонансные кривые. Таким образом величина Q характеризует остроту резонансной кривой. Согласно 4.3 чем больше отношение максимума энергии поля реактивного элемента к тепловой энергии , рассеиваемой за один период в резонансном контуре, тем острее резонансная кривая.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.