Овладение нарастающими перевозками на существующей железнодорожной линии, страница 3

 R - радиус кривой, определяемый по формуле:

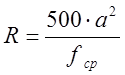            ,                                                     (2.6)

где  - средняя стрела прогиба круговой кривой;

переводной коэффициент, равный ;

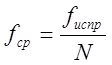                                      ,                                                     (2.7)

где количество точек (45);

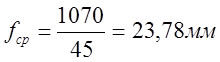
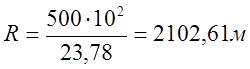
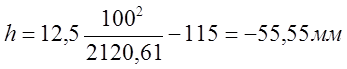
Принимаем

Длина круговой кривой определяется по формуле:

,                                                (2.8)

где - радиус момента инерции;

  - длина переходной кривой, дам.

Определим проектную стрелу в пределах круговой кривой

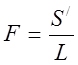                                                                                                            (2.9)

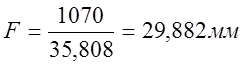
Округлим , тогда

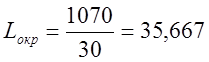
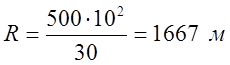
 2.2  Пикетаж характерных точек в кривой

К характерным точкам кривой относятся: начало круговой кривой (НКК), конец круговой кривой (ККК), начало переходной кривой входной (НПК), конец переходной кривой входной (КПК), конец переходной кривой выходной (КПК′), начало переходной кривой выходной (НПК′).

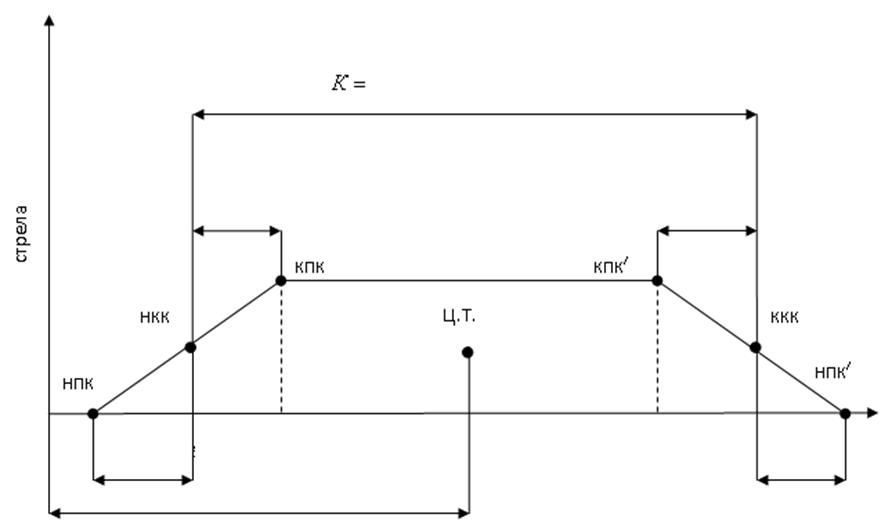
Рисунок 2.1- Пикетаж характерных точек в кривой

Положение характерных точек определяем по следующим зависимостям:

                                                НПК= 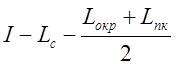,               (2.10)

                                                    НКК=НПК+ ,                (2.11)

                                                     КПК= НПК+,                (2.12)

                                                     ККК= НКК+ ,                 (2.13)

                                                     КПК′= ККК-,                (2.14)

                                                    НПК′= ККК+.               (2.15)

НПК₁ = 44 – 21,95-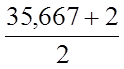 = 3,217 дам

НКК = 3,217 + 2/2 = 4,217 дам

КПК₁ = 4,217 + 2 = 6,217 дам

ККК = 4,217 + 35,667 = 39,884 дам

КПК₂= 39,884 – 2/2 = 38,884 дам

НПК₂= 39,884 + 2/2 = 30,884 дам

 2.3 Определение проектных стрел в каждой точке

Проектная стрела  равна 0, если 0≤ i ≤НПК;

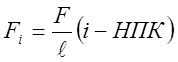, если НПК≤ i ≤ КПК,

i- номер точки, которая будет попадать в интервал;

, если КПК ≤ i ≤ КПК′.

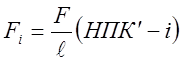, если КПК′ ≤ i ≤ НПК′.

Все невостребованные точки равны нулю.

Расчет проектных стрел в каждой точке кривой сведен в таблицу 2.1(графа 6). Невязка суммы 6 графы должна быть ±10 и разбрасывается по 1.

 2.4 Определение сдвижек в каждой точке кривой

Согласно теории нормалей сдвижка определяется:

                                                (2.16)

где  - значения графы 3 таблицы 2.1;

  - значения графы 6 таблицы 2.1;

сдвиг кривой в нулевой точке;

При выправке (реконструкции) кривой , то есть подходы к кривой остаются неизменными.

Для неизменяемости угла поворота существующей и проектной кривой, т.е.  для  должно выполняться условие:

1)  до 10 мм;

2)  отсюда следует ;

3) сдвижки начальной и конечной точки будут равны нулю, если .

Подсчёт проектных стрел, сдвижек, поправок к сдвижкам выполнен в табличной форме,

где графа №6-проектные стрелы, графа №7-разность проектных и натуральных стрел в каждой точке.

графа №8- удвоенная разность стрел,

графа №9- сумма удвоенных разностей,

графа №10- удвоенная сумма удвоенных разностей.

Нормаль в последней точке должна быть равна нулю, то невязка в последней точке неизбежна, так как  проектные стрелы принимались с точностью до 1мм. Полученная невязка распределена на все точки.

Сначала вводится поправка к проектным стрелам, стремясь к наибольшей их плавности, а затем определяется вызванное поправками изменение нормалей.

Если в первой точке кривой выбрана группа точек  со знаком  - , то часто в правой части кривой к проектным стрелам ввести поправки со знаком  +  для такого же количества точек.

Исходя из вышесказанного получена поправка к нормалям.

Поправки к нормалям вводятся следующим способом: полученную невязку δ распределяемна все точки

                                                  ,                                                              (2.17)

где δ- невязка в последней точке;