Проблема статистической обработки экспериментальных данных (Раздел 1 учебного пособия "Статистические методы обработки экспериментальных данных")

1. проблема статистической обработки экспериментальных данных

1.1. Наблюдение и измерение

Одним из основных способов изучения окружающего мира, средством познания было и остаётся наблюдение. Под наблюдением принято понимать целенаправленное восприятие свойств процессов и явлений. Опираясь на результаты наблюдения, исследователь строит физическую модель новых процессов и явлений, выдвигает научные гипотезы, создаёт теории, принимает решения. Наблюдение, как правило, сопровождается определённым преобразованием и регистрацией информации о свойствах наблюдаемого объекта.

Для повышения эффективности процесса наблюдения могут использоваться различные технические средства. Наблюдение присуще любому эксперименту. Фактически, эксперимент – это и есть создание условий для наиболее эффективного наблюдения тех или иных свойств изучаемого объекта. Поэтому каждый экспериментатор является в первую очередь наблюдателем. Учитывая большую, во многих случаях решающую роль эксперимента в современных науках, особенно в технических и экономических, можно утверждать, что понятие эксперимента является фундаментальным.

Принятие любого решения невозможно без наличия необходимой информации. Так, в случае управления нужна информация о состоянии управляемого объекта, окружающей среды и цели управления. Такая информация не может быть получена без наблюдения. В то же время от наблюдения до принятия решения информация претерпевает, как правило, существенные преобразования. Наиболее характерными этапами таких преобразований являются измерения и обработка результатов измерений.

В широком смысле измерение состоит в сравнении наблюдаемой величины с эталоном и получении в результате этого её численного значения. Если результаты наблюдений представлены количественно, то имело место измерение. Нередко, кроме измерения, различают подсчёт. Данную операцию можно квалифицировать как завершающий этап наблюдения – регистрацию величин дискретного типа (число студентов в аудитории, количество проросших зёрен на единице площади посева, доход работника фирмы и т.п.). Тогда измерения можно рассматривать как регистрацию величин непрерывного типа (вес, расстояние, скорость и т.д.).

Часто понятия наблюдения и измерения отождествляются. Представляется, что в рамках настоящей брошюры это не принципиально и вполне допустимо. Более того, без особой оговорки, используя как синонимы термины «наблюдение» и «измерение», будем включать в их содержание и подсчёт. Действительно, статистические методы обработки применимы к данным, получаемым как путём измерения, так и подсчёта. В дальнейшем, в силу указанных выше причин, все эти данные будут называться экспериментальными данными.

Говоря об экспериментальных данных, будем предполагать, что речь идёт о числовых величинах, векторах или функциях, т.е. о результатах количественных наблюдений, получаемых путём измерения или подсчёта. Если данные не могут быть представлены количественно, а являются качественными характеристиками, высказываниями, утверждениями, то их обработку следует предоставить специалистам по различным логическим методам.

Задачей обработки данных во многих случаях является принятие решения относительно значений определённых параметров (величин), характеризующих изучаемые явления или процессы. Обозначим эти параметры  a₁, a₂,..., a_m.  При этом возможны два случая. В первом из них непосредственно измеряются указанные величины. Говорят, что имеют место прямые измерения.

Во втором случае величины a₁, a₂,..., a_m непосредственно измерены быть не могут, а измеряются другие переменные x₁, x₂,..., x_n, с которыми функционально связаны величины a₁, a₂,..., a_m:

                                        x_i = f_i(a₁, a₂,..., a_m),   .           (1.1.1)

Выражение (1.1.1) в векторной форме запишем как

                                              ,                 (1.1.2)

где  ;  ;   .

Эти измерения называются косвенными. В общем случае функциональные связи (1.1.1) являются нелинейными. Если же схема косвенных измерений линейна, то имеют место соотношения

                                             ,                             

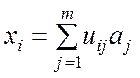или в векторно-матричной форме

                                                .                  (1.1.3)

Во многих случаях свойства объекта, над которым ставится эксперимент, изменяются с течением времени. Тогда соответственно вместо соотношений (1.1.2) и (1.1.3) при непрерывных измерениях имеем

                                              ,                          

                                             ,                         

а при дискретных измерениях

                                             ,                         

                                            .                         

Предполагается, что непрерывные и дискретные измерения проводятся в моменты времени, лежащие внутри интервала [0, T], т.е. t Î [0, T], t_i Î [0, T], .

Результат измерения всегда содержит ошибку (погрешность), представляющую собой отклонение результата измерения от истинного значения. Данное утверждение не относится в полной мере к подсчёту. Подсчитать количество интересующих объектов можно безошибочно. Так, в нормальных условиях можно точно определить количество компьютеров в интернет-классе. Редактор безошибочно может сосчитать число страниц рукописи и т.д. В то же время в некоторых условиях (дефицит времени, несовершенство средства наблюдения и др.) можно допустить ошибки при подсчёте. Например, с вертолёта трудно подсчитать точно количество коров в большом стаде.