Проблема статистической обработки экспериментальных данных (Раздел 1 учебного пособия "Статистические методы обработки экспериментальных данных"), страница 2

Существующая в настоящее время теория ошибок измерений развита в основном применительно к оцениванию непрерывных величин. При этом ошибки принято разделять на систематические и случайные.

Систематические ошибки – это составляющие общей ошибки, вызываемые факторами, действующими одинаковым образом при многократном повторении одних и тех же измерений. Эти ошибки при повторных измерениях остаются неизменными или, если изменяются, то закономерно. Систематические ошибки, как правило, обусловлены погрешностями измерительных приборов (инструментальные ошибки) и несовершенством методов измерений (методические ошибки).

Случайные ошибки – составляющие общей ошибки, изменяющиеся случайным образом при повторных измерениях одной и той же величины. Причиной случайных ошибок являются неконтролируемые факторы, проявление которых неодинаково в каждом измерении и которые заранее не могут быть учтены. Другими словами, случайные ошибки проявляются тогда, когда при измерениях имеют место случайные события. Объективно такие события при наблюдениях и измерениях происходят всегда, как бы ни повышалась «чистота» эксперимента.

Среди случайных ошибок особо следует выделить грубые ошибки (промахи). Их характер и причины существенно отличаются от характера других случайных ошибок измерений. Основная масса случайных ошибок появляется при исправно работающих средствах измерений и правильных действия экспериментатора. Причиной появления грубых ошибок являются неисправность приборов или неточность в работе экспериментатора.

В данной брошюре рассматриваются методы обработки экспериментальных данных, содержащих случайные ошибки (исключая грубые). Обозначим вектор ошибок через . Тогда при их аддитивном учёте и прямых измерениях выражение вектора экспериментальных данных принимает вид

                                             ;                (1.1.4)

в случае косвенных измерений

                                         .            (1.1.5)

При мультипликативном учёте ошибок можно записать

                                       ;          (1.1.6)

                        .                                                         (1.1.7)

1.2. Обобщённая модель обработки экспериментальных данных

Цель обработки данных эксперимента заключается в получении из них сведений о свойствах изучаемого объекта или процесса. На заключительном этапе экспериментатор принимает решение относительно этих свойств. Данное решение может быть связано, например, с оцениванием конкретных значений величин, характеризующих свойства объекта, а также с проверкой предположений о нахождении этих величин в определённых пределах, предположений о возможных законах распределения и т.д. Следует отметить, что процедура оценивания связана с получением оценок характеристик объекта. Под оценкой будем понимать приближённое значение оцениваемой величины, которое целесообразно принимать за её истинное значение. На рис.1.1 приведена обобщённая модель обработки экспериментальных данных.

Состояние (свойства) исследуемого объекта или процесса абстрагируется пространством ситуаций {E}. При этом под E Î {E} в общем случае понимается абстрактный параметр, характеризующий ситуацию, т.е. состояние объекта (фазовые координаты, структуру и т.д.). Абстрактный параметр может выражаться числом, функцией, функционалом, оператором, отношением, событием и т.п. Пространство ситуаций при оценивании вектора A_<m> представляет множество всех возможных его значений. Экспериментатора интересует истинное значение вектора A_<m>.

В процессе наблюдений регистрируется случайный вектор , который связан с вектором A выражениями (1.1.4) – (1.1.7). В общем виде истинную связь обозначим соотношением X = N(E). Случайные воздействия (помехи) , образующие пространство воздействий {}, искажают эту связь и она принимает вид .

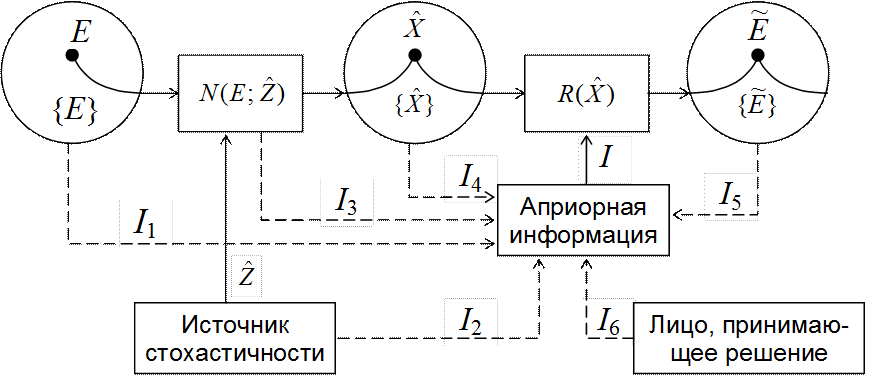
Рис.1.1. Обобщённая модель обработки экспериментальных данных

Помехи  генерируются источником стохастичности. Операция над параметром E и случайной величиной (процессом) , в результате которой формируется вектор , обозначена на схеме .