Проблема статистической обработки экспериментальных данных (Раздел 1 учебного пособия "Статистические методы обработки экспериментальных данных"), страница 5

Отдельное конкретное значение наблюдаемого основного признака называется его реализацией или вариантом. При статистическом исследовании вероятностных свойств совокупности объектов нет возможности производить опыты над каждым из них. Так, при изучении роста ежемесячных доходов граждан РФ невозможно установить доход каждого гражданина за ограниченное время. Для определения всхожести зерновых перед посевной бессмысленно пытаться обследовать каждое отдельное зерно. Всё же, несмотря на это, существует метод, который позволяет изучить интересующие свойства всей совокупности объектов. Речь идёт о выборочном методе, согласно которому основные признаки совокупности объектов изучаются по некоторой её части, называемой выборкой. Более строго в математической статистике выборкой называют совокупность наблюдаемых реализаций основного признака.

Совокупность всех возможных объектов (вариантов), из которых производится выборка, называется генеральной совокупностью. Следует отметить, что выборка является однородной, если все её элементы извлечены из одной генеральной совокупности.

Обычно предполагается, что выборки формируются при многократной реализации случайного эксперимента, результат которого нельзя заранее точно предсказать. Поэтому такие выборки называются случайными.

Пусть количественно исследуемый основной признак описывается случайной величиной . Допустим, что в процессе эксперимента получена последовательность из  n  значений  x₁,  x₂,…, x_n случайной величины . До проведения эксперимента эта последовательность является случайной выборкой и обозначается , ,…,.

Если основой признак наблюдаемого объекта описывается случайной функцией , то в процессе эксперимента получаем конечную совокупность реализаций  x₁(t),  x₂(t),…, x_n(t),  t Î [0; T] случайной  функции. Случайная выборка представляет в этом случае последовательность случайных функций , ,…,. Часто выборку целесообразно описывать с помощью n-мерного случайного вектора , компонентами которого являются элементы упорядоченной последовательности , ,…, .

Случайный характер выборки выражается в том, что нельзя заранее предсказать возможные значения её элементов, и любые две последовательности из n наблюдаемых значений в общем случае будут различными. В конкретных прикладных задачах элементы выборок представляют собой реализации случайных величин, т.е. детерминированные величины. Таким образом, априорно (до проведения эксперимента) выборка будет случайной, а апостериорно (после проведения опыта) – неслучайной.

Число n элементов выборки является конечным и называется объёмом выборки. Число элементов генеральной совокупности может быть конечным или бесконечным.

В статистике различают повторные и бесповторные выборки. Выборка называется повторной, если отобранный объект после испытания перед отбором следующего объекта снова возвращается в генеральную совокупность. Выборка называется бесповторной, если отобранный объект после испытания не возвращается в генеральную совокупность.

С позиций теории вероятностей элементы случайной выборки рассматриваются как независимые случайные величины с одной и той же функцией распределения  и плотностью распределения . Последнее означает, что для плотности распределения случайного вектора  имеет место равенство

                                            .                         

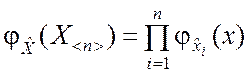Далеко не всякая выборка адекватно отражает свойства генеральной совокупности. Убедительный пример: требуется оценить средний рост жителей некоторого города, а в качестве выборки исследователю предлагают городскую баскетбольную команду. Нетрудно понять, насколько будет искажён результат.

Говорят, что выборка должна быть представительной или репрезентативной. Выборка представительна, если все элементы генеральной совокупности имеют одинаковую вероятность быть выбранными. Чтобы обеспечить это, не имея никаких сведений о генеральной совокупности, можно полагаться только на случайность отбора объектов в выборку. Все прочие способы будут необъективными, носящими следы влияния посторонних факторов. И семена для проверки всхожести, и жителей для оценивания среднего роста – всё нужно отбирать совершенно случайным образом. Иное дело, если экспериментатор заранее знает, что генеральная совокупность состоит из нескольких классов, различных по своим характеристикам. При таких условиях выборку лучше делать из каждого класса в отдельности. Например, изучая рост жителей, целесообразно делать отдельную выборку мужчин, отдельную женщин; при этом можно учесть возраст, профессию.