Проблема статистической обработки экспериментальных данных (Раздел 1 учебного пособия "Статистические методы обработки экспериментальных данных"), страница 6

Из случайного характера выборок неопровержимо следует, что любое суждение о генеральной совокупности по выборке само является случайным. Имеется в виду суждение, затрагивающее хотя бы один элемент генеральной совокупности, не попавший в выборку.

А какова же связь между наблюдениями, отбираемыми в состав экспериментальных данных, и выборочным методом? Имеется случайная величина  и в результате n независимых испытаний получаются n её допустимых значений. Если все допустимые значения случайной величины  считать генеральной совокупностью, то полученные при наблюдениях n значений образуют выборку. По этой выборке изучаются свойства случайной величины . Итак, производство наблюдений является частным случаем выборочного метода, когда в качестве генеральной совокупности берутся все допустимые значения некоторой случайной величины и исследуются свойства этой величины.

Если требуется исследовать несколько основных признаков, например рост и вес жителей города, три размера прямоугольных деталей, то экспериментатор наблюдает векторную случайную величину . При этом выборка ,,…, описывается nq-мерным случайным вектором .

Как уже отмечалось, случайные выборки используются для изучения свойств генеральной совокупности. При этом обычно элементы выборки используются для образования по соответствующим правилам новых случайных величин вида

                                    ,   j = 1,2,…

которые называются статистиками. Примерами статистик являются выборочная сумма 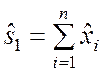, выборочное среднее  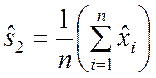и т.д.

Все свойства (характеристики) генеральной совокупности, получаемые на основе выборки, называются выборочными или статистическими (в отличие от теоретических, изучаемых в теории вероятностей). В дальнейшем все выборочные характеристики будут отмечаться индексом *. Так,  обозначает статистическую функцию распределения случайной величины ;  – статистическое математическое ожидание;  – статистическую дисперсию и т.д.  Все выборочные характеристики представляют собой функции элементов выборки, т.е. статистики.

В выборочном методе большое внимание уделяется изучению законов распределения различных статистик, статистических рядов. Теоретической основой выборочного метода являются предельные теоремы теории вероятностей, которые приведены в виде, адаптированном к рассматриваемой тематике, в § 2.2.

1.4. Задачи и методы обработки экспериментальных данных

Как уже отмечалось, основная цель обработки экспериментальных данных состоит в получении определённых сведений об исследуемом объекте (процессе, явлении). Особенности процесса обработки определяются характером решаемых задач и объёмом информации, получаемой в ходе эксперимента. По указанным признакам обработка может быть первичной и вторичной.

Задачами первичной обработки являются выделение полезного сигнала на фоне помех (шумов), сжатие данных и приведение их к системе измерений, пригодной для дальнейшей обработки или отображения. Наиболее характерной операцией выделения полезного сигнала является устранение грубых ошибок.

Задачи вторичной обработки могут быть распределены в две группы. Первая группа задач сводится к построению математических моделей реальных процессов и явлений, вторая группа – к анализу таких моделей. Математическая модель – это абстрактное информационное отражение реального процесса или явления на языке математики.

В кибернетике (как технической, так и экономической) и теории управления процедура построения математических моделей объектов управления по результатам наблюдения их входных и выходных процессов называется идентификацией. Параллельно с теорией идентификации в кибернетике развивается теория распознавания образов, которая также связана с проблематикой построения математических моделей по результатам обработки экспериментальных данных. Распознавание образов представляет собой задачу обработки данных, в процессе которой делается вывод о принадлежности распознаваемого образа к определённому классу. Этот класс и определяет вид искомой модели.

Наиболее типовыми задачами построения математических моделей на основе статистических методов являются задачи оценивания параметров (например, параметров законов распределения случайных объектов), оценивания неизвестных функциональных зависимостей (например, законов распределения), проверки гипотез, построения уравнений регрессии и распознавания образов.

В задачах анализа моделей производится оценка влияния множества факторов на конечный результат и выбор наиболее важных факторов, а также исследуется структура экспериментальных данных и построенных на их основе математических моделей.

Один из возможных вариантов перечня задач, решаемых при первичной и вторичной обработке показан на рис.1.2.

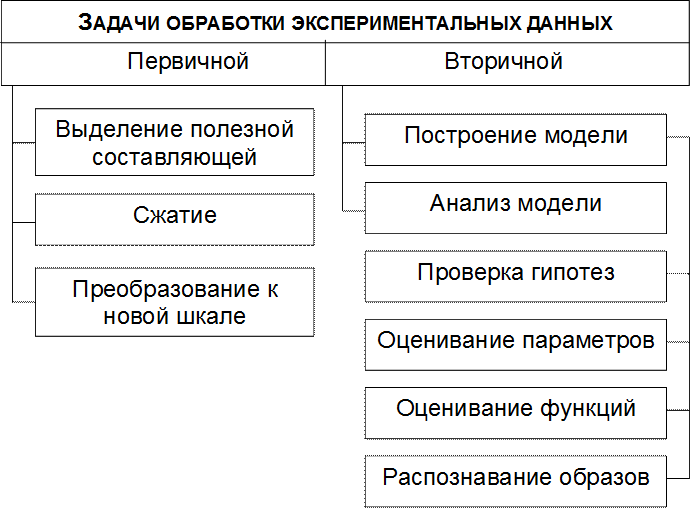
Рис.1.2. Классификация задач обработки экспериментальных данных