









Оценками законов распределения случайных величин являются статистические
законы распределения. Их построение осуществляется на основе
информации, содержащейся в выборке ![]() .
.
В дальнейшем, в рамках раздела 4 предполагается, что выборка
![]() простая, т.е. повторная выборка из
распределения
простая, т.е. повторная выборка из
распределения
![]() ,
,
где A<m> - вектор параметров распределения.
При проведении серии испытаний экспериментальные данные (выборка) представляются в виде табл.4.1, которая называется простым статистическим рядом.
Таблица 4.1
Простой статистический ряд
|
Номера испытаний |
1 |
2 |
3 |
… |
i |
… |
n |
|
Варианты признака |
x1 |
x2 |
x3 |
… |
xi |
… |
xn |
Если элементы случайной выборки упорядочены по возрастанию, т.е.
x1 £ x2 £ x3 £…£ xi £…£ xn,
получаемая таблица называется вариационным рядом. Разность wn = xn – x1 между наибольшим и наименьшим элементами вариационного ряда называется размахом выборки.
Вариационный ряд является простейшей формой статистического закона распределения, который определяется в результате эксперимента.
Если наблюдаемый случайный признак является дискретным, или точность измерений ограничена, или результаты наблюдений округляются, значения некоторых вариантов признака в выборке могут совпадать. Множества совпадающих вариантов наблюдаемого признака называются связками. Из этого следует, что различные варианты могут появляться с разной частотой.
Таблица 4.2
Вариационный ряд с вариантами различной частоты
|
Варианты признака |
x1 |
x2 |
x3 |
… |
xl |
… |
xn |
|
Частота вариантов |
m1/n |
m2/n |
m3/n |
… |
ml/n |
… |
mn/n |
В табл. 4.2 представлен вариационный ряд, в котором ml – число появлений в выборке варианта xl; ![]() – частота варианта xl,
– частота варианта xl, ![]() . Такой ряд можно
рассматривать как ряд распределения некоторой дискретной случайной величины.
. Такой ряд можно
рассматривать как ряд распределения некоторой дискретной случайной величины.
Пример 4.1. Проведены испытания 12 однотипных микросхем и с точностью до 1 часа зарегистрировано время безотказной работы каждой из них. Результаты испытаний сведены в простой статистический ряд.
Таблица 4.3
Простой статистический ряд (к примеру 4.1)
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
ti, ч |
30 |
108 |
36 |
69 |
117 |
161 |
143 |
500 |
108 |
135 |
89 |
36 |
На основе простого статистического ряда, табл.4.3, построен вариационный ряд.
Таблица 4.4
Вариационный ряд (к примеру 4.1)
|
l |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
tl, ч |
30 |
36 |
36 |
69 |
89 |
108 |
108 |
117 |
135 |
143 |
161 |
500 |
Массив данных в табл. 4.4 может быть представлен вариационным рядом с частотами вариантов.
Таблица 4.5
Вариационный ряд с частотами вариантов (к примеру 4.1)
|
tl, ч |
30 |
36 |
69 |
89 |
108 |
117 |
135 |
143 |
161 |
500 |
|
|
1/12 |
2/12 |
1/12 |
1/12 |
2/12 |
1/12 |
1/12 |
1/12 |
1/12 |
1/12 |
Из табл.4.5 видно, что в выборке содержатся две связки, в каждую из которых входит два варианта.
По распределению величины ![]() –
времени безотказной работы микросхем, можно судить о распределении генеральной
совокупности, тем точнее и надёжнее, чем больше объём n
выборки.
–
времени безотказной работы микросхем, можно судить о распределении генеральной
совокупности, тем точнее и надёжнее, чем больше объём n
выборки.
При большом объёме выборки из генеральной совокупности, наблюдаемый
признак которой имеет непрерывное распределение, вариационный ряд
(табл. 4.2) становится громоздким. В этом случае диапазон наблюдаемых
вариантов xi разбивают на интервалы,
называемые разрядами, вычисляют частоты ![]() попадания
вариантов случайной величины
попадания
вариантов случайной величины ![]() в эти разряды и
представляют результаты в виде табл. 4.6. Эта таблица называется интервальным
вариационным или статистическим рядом случайной величины
в эти разряды и
представляют результаты в виде табл. 4.6. Эта таблица называется интервальным
вариационным или статистическим рядом случайной величины
![]() .
.
Таблица 4.6
Интервальный вариационный ряд
|
Jl |
x1; x2 |
x2; x3 |
… |
xl; xl+1 |
… |
xr; xr+1 |
|
ml |
m1 |
m2 |
… |
ml |
… |
mr |
|
|
|
|
… |
|
… |
|
В представленной таблице Jl = [xl; xl+1) – l-й разряд; ml
– число значений (вариантов) случайной величины ![]() ,
попавших в l-й разряд; xl; xl+1
– границы l-го разряда; r
– число разрядов;
,
попавших в l-й разряд; xl; xl+1
– границы l-го разряда; r
– число разрядов; ![]() = ml/n = P*(xl £ xi<
xl+1),
= ml/n = P*(xl £ xi<
xl+1), ![]() .
.
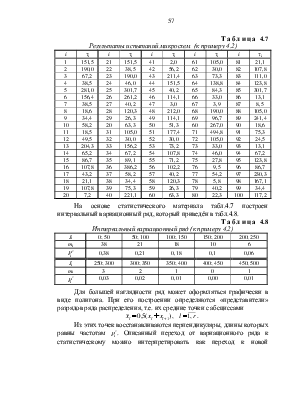
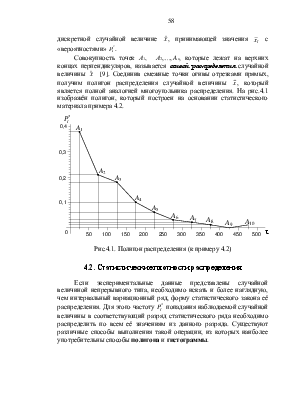
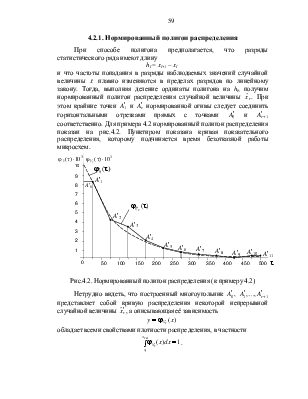
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.