Оценивание законов распределения случайных величин (Раздел 4 учебного пособия "Статистические методы обработки экспериментальных данных"), страница 3

На основе статистического материала табл.4.7 построен интервальный вариационный ряд, который приведён в табл.4.8.

Таблица 4.8

Интервальный вариационный ряд (к примеру 4.2)

Jl	0; 50	50; 100	100; 150	150; 200	200; 250
ml	38	21	18	10	6
	0,38	0,21	0,18	0,1	0,06
Jl	250; 300	300; 350	350; 400	400; 450	450; 500
ml	3	2	1	0	1
	0,03	0,02	0,01	0,00	0,01

Для большей наглядности ряд может оформляться графически в виде полигона. При его построении определяются «представители» разрядов ряда распределения, т.е. их средние точки с абсциссами

                                         ,   .

Из этих точек восстанавливаются перпендикуляры, длины которых равны частотам . Описанный переход от вариационного ряда к статистическому можно интерпретировать как переход к новой дискретной случайной величине , принимающей значения  с «вероятностями» .

Совокупность точек А₁,  А₂,…, A_r, которые лежат на верхних концах перпендикуляров, называется огивой распределения случайной величины   [9]. Соединив смежные точки огивы отрезками прямых, получим полигон распределения случайной величины , который является полной аналогией многоугольника распределения. На рис.4.1 изображён полигон, который построен на основании статистического материала примера 4.2.

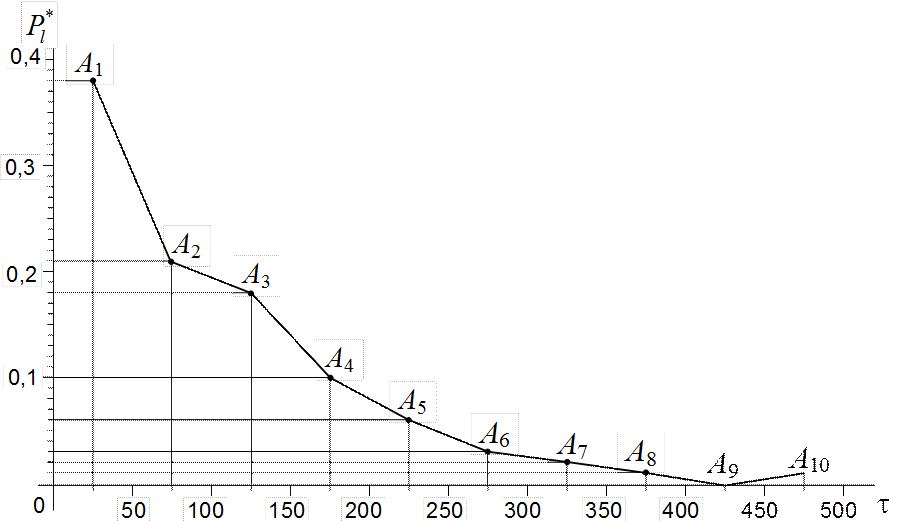
Рис.4.1. Полигон распределения (к примеру 4.2)

4.2. Статистические плотности распределения

Если экспериментальные данные представлены случайной величиной непрерывного типа, необходимо искать и более наглядную, чем интервальный вариационный ряд, форму статистического закона её распределения. Для этого частоту  попадания наблюдаемой случайной величины в соответствующий разряд статистического ряда необходимо распределить по всем её значениям из данного разряда. Существуют различные способы выполнения такой операции, из которых наиболее употребительны способы полигона и гистограммы.

4.2.1. Нормированный полигон распределения

При способе полигона предполагается, что разряды статистического ряда имеют длину

                                                      h_l = x_l+1 – x_l  

и что частоты попадания в разряды наблюдаемых значений случайной величины  плавно изменяются в пределах разрядов по линейному закону. Тогда, выполняя деление ординаты полигона на h_l, получим нормированный полигон распределения случайной величины . При этом крайние точки  и  нормированной огивы следует соединить горизонтальными отрезками прямых с точками  и  соответственно. Для примера 4.2 нормированный полигон распределения показан на рис.4.2. Пунктиром показана кривая показательного распределения, которому подчиняется время безотказной работы микросхем.

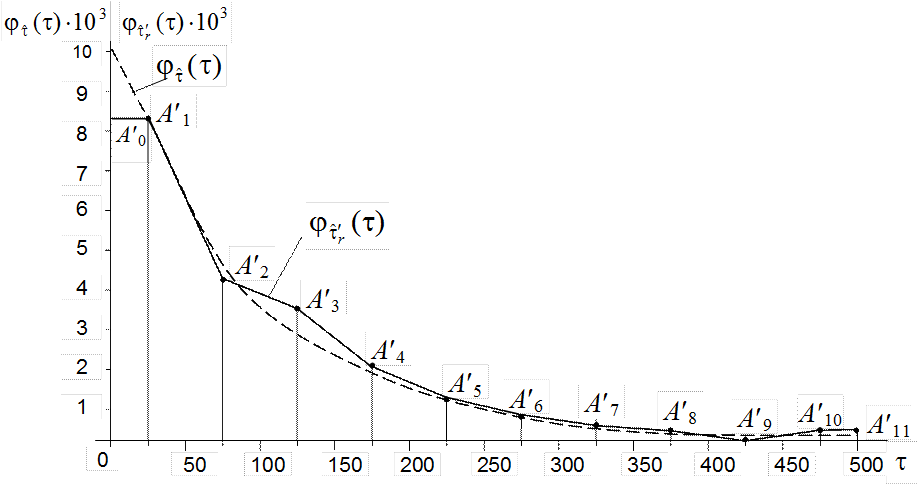
Рис.4.2. Нормированный полигон распределения (к примеру 4.2)

Нетрудно видеть, что построенный многоугольник , ,…, представляет собой кривую распределения некоторой непрерывной случайной величины , а описывающая её зависимость

                                                    

обладает всеми свойствами плотности распределения, в частности

                                                  .

4.2.2. Гистограмма распределения

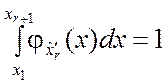При способе гистограммы предполагается, что в пределах l-го разряда статистического ряда плотность распределения непрерывной случайной величины  постоянна и равна

                                                    ,

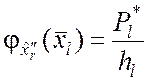где h_l = x_l+1 – x_l – длина l-го разряда.