Математика \ Статистические методы обработки экспериментальных данных

Оценивание законов распределения случайных величин (Раздел 4 учебного пособия "Статистические методы обработки экспериментальных данных"), страница 4

Проводя через точки , ,…, нормированной огивы горизонтальные отрезки прямых, получают семейство прямоугольников, называемое гистограммой распределения случайной величины . На рис.4.3 приведена гистограмма по данным примера 4.2. Для сравнения там же пунктиром изображена теоретическая кривая показательного распределения. Легко заметить, что площади прямоугольников, составляющих гистограмму, равны соответствующим частотам, а площадь всей гистограммы равна единице:

                                                  .

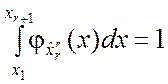Следовательно, огибающая гистограммы обладает свойствами кривой распределения, а описывающая её зависимость

                                                     

имеет свойства плотности распределения.

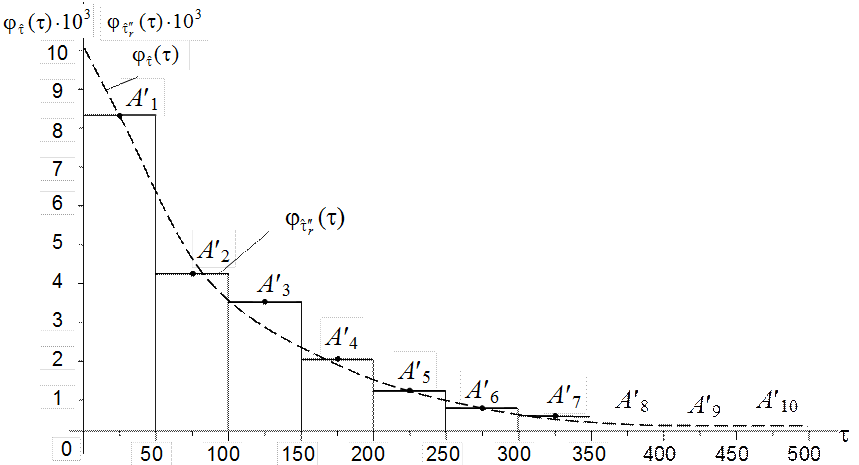
Рис.4.3. Гистограмма распределения (к примеру 4.2)

С увеличением объёма n выборки и, следовательно, числа разрядов статистического ряда огибающие полигона  и гистограммы  всё более приближаются к кривой распределения  случайной величины . Таким образом, они могут использоваться для приближённого описания плотности её распределения:

                                                                    

или

                                            .                        

4.3. Статистические функции распределения

4.3.1. Выборочная функция распределения

По вариационному ряду табл.4.2 можно построить статистическую или выборочную функцию распределения  случайной величины .

По определению

                                   .

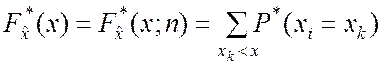Следовательно, в явном виде статистическая функция распределения примет вид

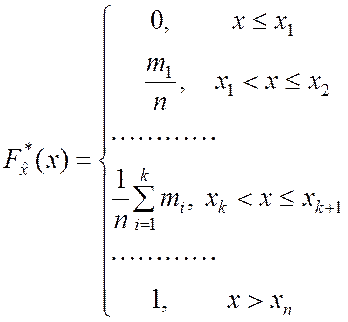                                     .        (4.3.1)

График функции (4.3.1) в условиях примера 4.1 показан на рис.4.4. Обоснованием применимости функции  для оценивания истинной функции распределения  случайной величины  служит предельная теорема В.И. Гливенко, которая формулируется следующим образом.

При увеличении объёма n выборки статистическая функция распределения  неограниченно приближается (сходится по вероятности) к истинной функции распределения  случайной величины :

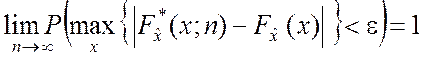,    e > 0.                                                           (4.3.2)

Таким образом,  – состоятельная оценка . Известно также, что функция  является несмещённой оценкой для  :

                                     .                           

Рис.4.4. Статистическая функция распределения (к примеру 4.1)

В силу соотношения (4.3.2) дисперсия с ростом n уменьшается, следовательно, эта оценка является асимптотически эффективной. Отсюда вытекает, что при достаточно большом массиве экспериментальных данных функцию распределения изучаемой случайной величины можно приближённо заменять её выборочной функцией распределения.

4.3.2. Кумулята распределения

Используя полигон или гистограмму, можно построить статистическую функцию распределения (так называемую кумуляту распределения случайной величины) путём интегрирования функции :

                                  .              

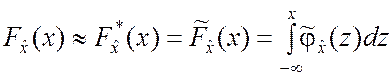При численном интегрировании получим

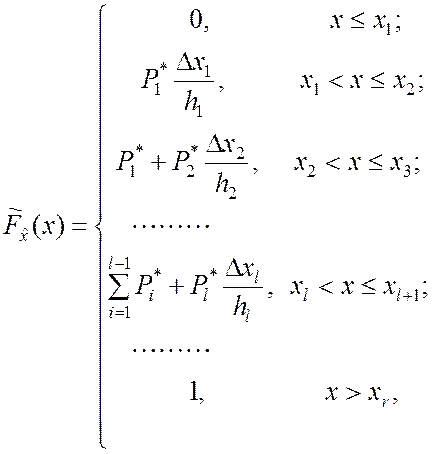                                   (4.3.3)

где   hl = xl+1 – xl,   Dxl = x – xl.

График функции (4.3.3) в условиях примера 4.2 показан на рис.4.5, на котором пунктиром изображён график теоретической функции показательного закона распределения.

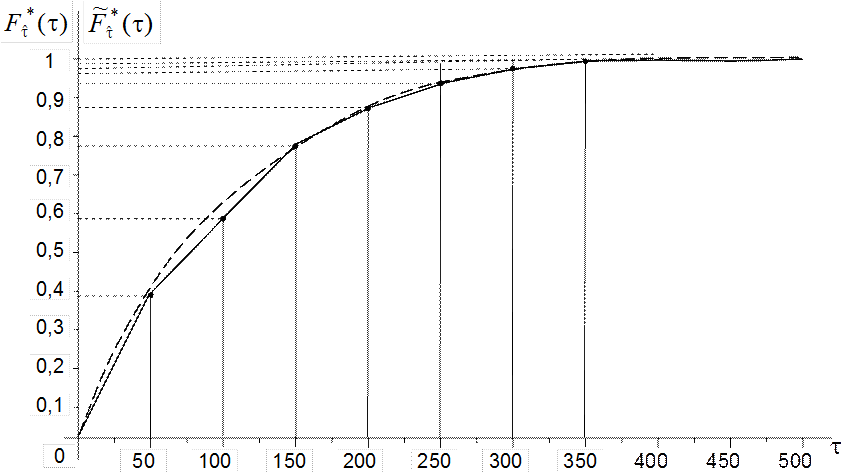
Рис.4.5. Кумулята распределения (к примеру 4.2)

Примечание. Поскольку функция распределения дискретной случайной величины ступенчатая, то её оценка может иметь лишь форму рис.4.4. Другими словами для дискретной случайной величины кумуляты не существует.

4.3.4. Качество оценивания функций распределения

Скачать файл